
| A. | $[{0,\left.{\frac{π}{6}}]}\right.$ | B. | $[{0,\left.{\frac{π}{3}}]}\right.$ | C. | $[{0,\left.{\frac{π}{4}}]}\right.$ | D. | $[{\frac{π}{6},\left.{\frac{π}{4}}]}\right.$ |
分析 求导数,利用函数f(x)=2x3+3|a|x2+6a•bx+7在实数集R上单调递增,可得判别式小于等于0在R上恒成立,再利用$|{\vec a}|=2\sqrt{2}|{\vec b}|≠0$,利用向量的数量积,即可得到结论.
解答 解:求导数可得f′(x)=6x2+6|$\overrightarrow{a}$|x+6$\overrightarrow{a}•\overrightarrow{b}$,则由函数f(x)=2x3+3|a|x2+6a•bx+7在实数集R上单调递增,
可得f′(x)=6x2+6|$\overrightarrow{a}$|x+6$\overrightarrow{a}•\overrightarrow{b}$≥0恒成立,即 x2+|$\overrightarrow{a}$|x+$\overrightarrow{a}•\overrightarrow{b}$≥0恒成立,
故判别式△=$\overrightarrow{a}$2-4$\overrightarrow{a}•\overrightarrow{b}$≤0 恒成立,
再由$|{\vec a}|=2\sqrt{2}|{\vec b}|≠0$,可得8|$\overrightarrow{b}$|2≤8$\sqrt{2}$|$\overrightarrow{b}$|2cos<$\vec a$,$\vec b$>,
∴cos<$\vec a$,$\vec b$>≥$\frac{\sqrt{2}}{2}$,
∴<$\vec a$,$\vec b$>∈[0,$\frac{π}{4}$],
故选:C.
点评 本题考查导数知识的运用,考查函数的单调性,考查向量的数量积,解题的关键是利用判别式小于等于0在R上恒成立,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos2α>0 | B. | tan2α>0 | C. | $cos\frac{α}{2}>0$ | D. | $tan\frac{α}{2}>0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
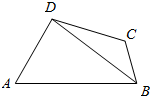 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com