
【题目】已知函数 ![]() .
.
(1)求f(x)单调递增区间;
(2)△ABC中,角A,B,C的对边a,b,c满足 ![]() ,求f(A)的取值范围.
,求f(A)的取值范围.
【答案】
(1)解:f(x)= ![]() ﹣
﹣ ![]() +
+ ![]() sin2x=
sin2x= ![]() sin2x﹣
sin2x﹣ ![]() cos2x=sin(2x﹣
cos2x=sin(2x﹣ ![]() ),
),
令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,得到﹣
,k∈Z,得到﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
则f(x)的增区间为[﹣ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z);
+kπ](k∈Z);
(2)解:由余弦定理得:cosA= ![]() ,即b2+c2﹣a2=2bccosA,
,即b2+c2﹣a2=2bccosA,
代入已知不等式得:2bccosA> ![]() bc,即cosA>
bc,即cosA> ![]() ,
,
∵A为△ABC内角,
∴0<A< ![]() ,
,
∵f(A)=sin(2A﹣ ![]() ),且﹣
),且﹣ ![]() <2A﹣
<2A﹣ ![]() <
< ![]() ,
,
∴﹣ ![]() <f(A)<
<f(A)< ![]() ,
,
则f(A)的范围为(﹣ ![]() ,
, ![]() ).
).
【解析】(1)f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化简为一个角的正弦函数,利用正弦函数的增减性确定出f(x)的单调增区间即可;(2)利用余弦定理表示cosA,整理后代入已知不等式求出cosA的范围,进而求出A的范围,即可确定出f(A)的范围.
【考点精析】关于本题考查的两角和与差的正弦公式和正弦函数的单调性,需要了解两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能得出正确答案.
上是减函数才能得出正确答案.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρsin(θ+
(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρsin(θ+ ![]() )=2
)=2 ![]() (Ⅰ)直接写出C1的普通方程和极坐标方程,直接写出C2的普通方程;
(Ⅰ)直接写出C1的普通方程和极坐标方程,直接写出C2的普通方程;
(Ⅱ)点A在C1上,点B在C2上,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ=2acosθ(a>0),直线l的参数方程为 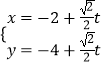 (t为参数),直线l与曲线C相交于A,B两点.
(t为参数),直线l与曲线C相交于A,B两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若|AB|=2 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=[ax2﹣(2a+1)x+a+2]ex(a∈R).
(1)当a≥0时,讨论函数f(x)的单调性;
(2)设g(x)= ![]() ,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩阵A的变换下,坐标平面上的点的横坐标伸长到原来的3倍,纵坐标不变.
(1)求矩阵A及A﹣1;
(2)求圆x2+y2=4在矩阵A﹣1的变换下得到的曲线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)若存在x0∈[ ![]() ,e](e是自然对数的底数,e=2.71828…),使不等式2f(x0)≥g(x0)成立,求实数a的取值范围.
,e](e是自然对数的底数,e=2.71828…),使不等式2f(x0)≥g(x0)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|. (Ⅰ)求不等式f(x)≥﹣2的解集M;
(Ⅱ)对任意x∈[a,+∞),都有f(x)≤x﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求: (Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取球次数ξ的概率分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com