
【题目】已知函数f(x)=ex﹣ax有极值1,这里e是自然对数的底数.
(1)求实数a的值,并确定1是极大值还是极小值;
(2)若当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立,求实数m的取值范围.
【答案】
(1)解:f′(x)=ex﹣a,∵函数f(x)=ex﹣ax有极值1,
∴存在x0,使得f′(x0)= ![]() ﹣a=0,f(x0)=
﹣a=0,f(x0)= ![]() ﹣ax0=1,
﹣ax0=1,
解得x0=0,a=1.
∴f′(x)=ex﹣1,可知:0是极小值点,因此1是极小值.
(2)解:当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立ex﹣x﹣1﹣mxln(x+1)≥0恒成立.
令g(x)=ex﹣(x+1),x≥0.g(0)=0.
则g′(x)=ex﹣1≥0,
∴x≥0时,函数g(x)单调递增,因此g(x)≥g(0)=0,因此ex≥x+1.
①若mxln(x+1)+x+1≤x+1,则ex﹣x﹣1﹣mxln(x+1)≥0恒成立.
则mxln(x+1)≤0,可得:m≤0.
∴m≤0时,x≥0时,f(x)≥mxln(x+1)+1恒成立.
②m>0时,x≥0时,mxln(x+1)+x+1≤ex.
令F(x)=mxln(x+1)+x+1﹣ex,(x≥0),F(0)=0.
由F(x)≤0,可得mxln(x+1)≤ex﹣x﹣1,
x=0时,化为0≤0,恒成立,m∈R.
x>0时,化为:m≤ 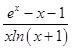 .
.
下面证明: ![]() ≤
≤ 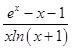 .
.
令h(x)=2ex﹣2x﹣2﹣xln(x+1),h(0)=0.
h′(x)=2ex﹣2﹣ln(x+1)﹣ ![]() .h′(0)=0.
.h′(0)=0.
h″(x)=2ex﹣ ![]() ﹣
﹣ ![]() ≥h″(0)=0,
≥h″(0)=0,
∴h′(x)≥0.
∴函数h(x)在[0,+∞)上单调递增,∴h(x)≥h(0)=0.
因此: ![]() ≤
≤ 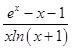 成立,并且
成立,并且 ![]() 是其最小值.
是其最小值.
∴m≤ ![]() .
.
综上可得:实数m的取值范围是 ![]() .
.
【解析】(1)f′(x)=ex﹣a,根据函数f(x)=ex﹣ax有极值1,可得存在x0,使得f′(x0)= ![]() ﹣a=0,f(x0)=
﹣a=0,f(x0)= ![]() ﹣ax0=1,解得x0,a.即可判断出结论.(2)当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立ex﹣x﹣1﹣mxln(x+1)≥0恒成立.令g(x)=ex﹣(x+1),x≥0.g(0)=0.利用导数研究其单调性可得:ex≥x+1.①若mxln(x+1)+x+1≤x+1,则ex﹣x﹣1﹣mxln(x+1)≥0恒成立.可得:m≤0.②m>0时,x≥0时,mxln(x+1)+x+1≤ex.令F(x)=mxln(x+1)+x+1﹣ex,(x≥0),F(0)=0.
﹣ax0=1,解得x0,a.即可判断出结论.(2)当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立ex﹣x﹣1﹣mxln(x+1)≥0恒成立.令g(x)=ex﹣(x+1),x≥0.g(0)=0.利用导数研究其单调性可得:ex≥x+1.①若mxln(x+1)+x+1≤x+1,则ex﹣x﹣1﹣mxln(x+1)≥0恒成立.可得:m≤0.②m>0时,x≥0时,mxln(x+1)+x+1≤ex.令F(x)=mxln(x+1)+x+1﹣ex,(x≥0),F(0)=0.
由F(x)≤0,可得mxln(x+1)≤ex﹣x﹣1,x>0时,化为:m≤ ![]() .下面证明:
.下面证明: ![]() ≤
≤ ![]() .利用导数研究其单调性即可得出.
.利用导数研究其单调性即可得出.
【考点精析】关于本题考查的函数的极值与导数和函数的最大(小)值与导数,需要了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点
的右焦点 ![]() ,且经过点
,且经过点 ![]() ,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)
,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方) 
(1)求椭圆C的方程;
(2)若|AM|=2|MB|,且直线l与圆 ![]() 相切于点N,求|MN|的长.
相切于点N,求|MN|的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() x2﹣(1+a)x.
x2﹣(1+a)x.
(1)求函数f(x)的单调区间;
(2)若f(x)≥0对定义域中的任意x恒成立,求实数a的取值范围;
(3)证明:对任意正整数m,n,不等式 ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的点A(4,t)到其焦点F的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F作直线l,使得抛物线C上恰有三个点到直线1的距离为2,求直线1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示. 
(1)求证:DE∥平面BCC1B1;
(2)求DE与平面ABC所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1 , 则双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA1的长为5. 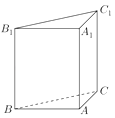
(1)求三棱柱ABC﹣A1B1C1的体积;
(2)设M是BC中点,求直线A1M与平面ABC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一期间,某商场决定从2种服装、3种家电、4种日用品中,选出3种商品进行促销活动.
(1)试求选出3种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高60元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为n元的奖金;若中两次奖,则获得数额为3n元的奖金;若中三次奖,则共获得数额为 6n元的奖金.假设顾客每次抽奖中奖的概率都是 ![]() ,请问:商场将奖金数额n最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额n最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com