
【题目】下列四种说法正确的是( )
①函数f(x)的定义域是R,则“x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的充要条件;
②命题“ ![]() ”的否定是“
”的否定是“ ![]() ”;
”;
③命题“若x=2,则x2﹣3x+2=0”的逆否命题是真命题;
④p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数,则p∧q为真命题.
A.①②③④
B.②③
C.③④
D.③
【答案】D
【解析】解:①函数f(x)的定义域是R,
则“x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的必要不充分条件,故错误;
②命题“ ![]() ”的否定是“
”的否定是“ ![]() ”,故错误;
”,故错误;
③命题“若x=2,则x2﹣3x+2=0”是真命题,故它的逆否命题是真命题,故正确;
④p:在△ABC中,若cos2A=cos2B,即1﹣2sin2A=1﹣2sin2B,sinA=sinB,则A=B,故p为真命题;
q:y=sinx在第一象限是增函数是假命题,则p∧q为假命题,故错误.
所以答案是:D .
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系,以及对二倍角的余弦公式的理解,了解二倍角的余弦公式:![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC的直角顶点A在y轴上,点B(1,0),D为斜边BC的中点,且AD平行于x轴.
(1)求点C的轨迹方程;
(2)设点C的轨迹为曲线Γ,直线BC与Γ的另一个交点为E,以CE为直径的圆交y轴于点M,N,记圆心为P,∠MPN=α,求α的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为4π,则( )
的最小正周期为4π,则( )
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于直线 ![]() 对称
对称
C.函数f(x)图象上的所有点向右平移 ![]() 个单位长度后,所得的图象关于原点对称
个单位长度后,所得的图象关于原点对称
D.函数f(x)在区间(0,π)上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B是海面上两个固定观测站,现位于B点南偏东45°且相距 ![]() 海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距
海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距 ![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足a1 , 2a2 , a3+6成等差数列,且a42=9a1a5 .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非零平面向量 ![]() ,
, ![]() ,则“|
,则“| ![]() |=|
|=| ![]() |+|
|+| ![]() |”是“存在非零实数λ,使
|”是“存在非零实数λ,使 ![]() =λ
=λ ![]() ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.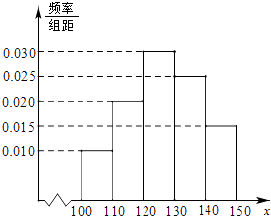
(Ⅰ)将T表示为X的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com