
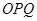 是半径为1,圆心角为
是半径为1,圆心角为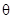 的扇形,
的扇形,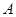 是扇形弧
是扇形弧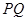 上的动点,
上的动点,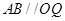 ,
,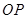 与
与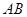 交于点
交于点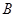 ,
,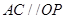 ,
,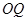 与
与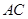 交于点
交于点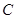 .记
.记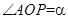 .
.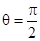 ,如图3,当角
,如图3,当角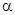 取何值时,能使矩形
取何值时,能使矩形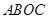 的面积最大;
的面积最大;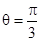 ,如图4,当角
,如图4,当角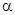 取何值时,能使平行四边形
取何值时,能使平行四边形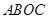 的面积最大.并求出最大面积.
的面积最大.并求出最大面积.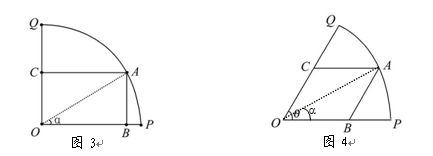
科目:高中数学 来源:不详 题型:解答题
 ,
, 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A, 和
和 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| s |
| 3 |
| t |
| C |
| 2 |
| s |
| t |
| 1 |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
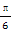 )-sin2x.
)-sin2x.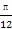 )的值.
)的值.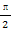 ],都有f(x)≤c,求实数c的取值范围.
],都有f(x)≤c,求实数c的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com