
【题目】一个圆经过点![]() ,且和直线
,且和直线![]() 相切.
相切.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)已知点![]() ,设不垂直于
,设不垂直于![]() 轴的直线
轴的直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 轴是
轴是![]() 的角平分线,证明直线
的角平分线,证明直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)圆心到定点![]() 与到定直线
与到定直线![]() 的距离相等,可知圆心的轨迹是以点
的距离相等,可知圆心的轨迹是以点![]() 为焦点的抛物线,求出方程即可;
为焦点的抛物线,求出方程即可;
(2)易知直线![]() 斜率存在且不为零,可设直线
斜率存在且不为零,可设直线![]() ,设
,设![]() ,
,![]() ,联立直线
,联立直线![]() 与抛物线方程,可得关于
与抛物线方程,可得关于![]() 的一元二次方程,由
的一元二次方程,由![]() 轴是
轴是![]() 的角平分线,可得
的角平分线,可得![]() ,整理可求得
,整理可求得![]() ,再结合韦达定理
,再结合韦达定理![]() ,从而可求得
,从而可求得![]() 的值,进而可求得直线
的值,进而可求得直线![]() 过定点.
过定点.
(1)由题意,圆心到定点![]() 与到定直线
与到定直线![]() 的距离相等,
的距离相等,
根据抛物线的定义可知,圆心的轨迹是以点![]() 为焦点的抛物线,其方程为
为焦点的抛物线,其方程为![]() .
.
(2)由题可知,直线![]() 与C有两个交点且不垂于于
与C有两个交点且不垂于于![]() 轴,
轴,
所以直线![]() 斜率存在且不为零,设直线
斜率存在且不为零,设直线![]() ,
,![]() ,
,![]() ,
,
联立![]() ,可得
,可得![]() ,
,
则![]() ,且
,且![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 轴是
轴是![]() 的角平分线,
的角平分线,
所以![]() ,整理可得
,整理可得![]() ,
,
所以![]() ,即
,即![]() ,此时满足
,此时满足![]() ,故
,故![]() :
:![]() ,
,
所以,直线PQ过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正三棱锥![]() 每个顶点都在球
每个顶点都在球![]() 的球面上,球心
的球面上,球心![]() 在正三棱锥的内部.球的半径为
在正三棱锥的内部.球的半径为![]() ,且
,且![]() .若过
.若过![]() 作球
作球![]() 的截面,所得圆周长的最大值是
的截面,所得圆周长的最大值是![]() ,则该三棱锥的侧面积为_______.
,则该三棱锥的侧面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1995年联合国教科文组织把每年4月23日确定为“世界读书日”,为提升学生的文化素养,养成多读书、读好书的文化生活习惯,某中学开展图书源流活动,让图书发挥它的最大价值,该校某班图书角有文学名著类图书5本,学科辅导书类图书3本,其它类图书2本,共10本不同的图书,该班班委会从图书角的10本不同的图书中随机挑选3本不同的图书参加学校的图书漂流活动。
(I)求选出的三本图书来自于两个不同类别的概率:
(II)设随机变量![]() 表示选出的3本图书中,文学名著类本数与学科辅导类本数差的绝对值,求随机变量
表示选出的3本图书中,文学名著类本数与学科辅导类本数差的绝对值,求随机变量![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点,且面积最小的圆方程为( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代社会,“鼠标手”已成为常见病,一次实验中,10名实验对象进行160分钟的连续鼠标点击游戏,每位实验对象完成的游戏关卡一样,鼠标点击频率平均为180次/分钟,实验研究人员测试了实验对象使用鼠标前后的握力变化,前臂表面肌电频率(![]() )等指标.
)等指标.
(I)10 名实验对象实验前、后握力(单位:![]() )测试结果如下:
)测试结果如下:
实验前:346,357,358,360,362,362,364,372,373,376
实验后:313,321,322,324,330,332,334,343,350,361
完成茎叶图,并计算实验后握力平均值比实验前握力的平均值下降了多少![]() ?
?
(Ⅱ)实验过程中测得时间![]() (分)与10名实验对象前臂表面肌电频率(
(分)与10名实验对象前臂表面肌电频率(![]() )的中的位数
)的中的位数![]() (
(![]() )的九组对应数据
)的九组对应数据![]() 为
为![]() ,
,![]() .建立
.建立![]() 关于时间
关于时间![]() 的线性回归方程;
的线性回归方程;
(Ⅲ)若肌肉肌电水平显著下降,提示肌肉明显进入疲劳状态,根据(Ⅱ)中9组数据分析,使用鼠标多少分钟就该进行休息了?
参考数据:![]() ;
;
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
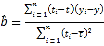 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是圆
是圆![]() :
:![]() 上的动点,定点
上的动点,定点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,记
,记![]() 点的轨迹为
点的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 的方程;
的方程;
(Ⅱ)若动直线![]() :
:![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,点
,点![]() 在轨迹
在轨迹![]() 上,且四边形
上,且四边形![]() 为平行四边形.证明:四边形
为平行四边形.证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com