
【题目】中国农历的“二十四节气”是凝结着中华民族的智慧与传统文化的结晶,“二十四节气”歌是以“春、夏、秋、冬”开始的四句诗,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气”歌,只能说出春夏两句的有45人,能说出春夏秋三句及其以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出第一句“春”或一句也说不出的大约有( )
A.69人B.84人C.108人D.115人
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,
中,底面ABCD为矩形,![]() ,
,![]() ,侧面SAD是以AD为斜边的等腰直角三角形,且平面
,侧面SAD是以AD为斜边的等腰直角三角形,且平面![]() 平面ABCD,M,N分别为AD,SC的中点.
平面ABCD,M,N分别为AD,SC的中点.
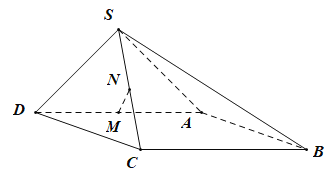
(1)求证:![]() 平面SAB.
平面SAB.
(2)求直线BN与平面SAB所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为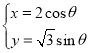 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,一场新冠肺炎疫情突如其来,在党中央强有力的领导下,全国各地的医务工作者迅速驰援湖北,以大无畏的精神冲在了抗击疫情的第一线,迅速控制住疫情.但国外疫情严峻,输入性病例逐渐增多,为了巩固我国的抗疫成果,保护国家和人民群众的生命安全,我国三家生物高科技公司各自组成A、B、C三个科研团队进行加急疫苗研究,其研究方向分别是灭活疫苗、核酸疫苗和全病毒疫苗,根据这三家的科技实力和组成的团队成员,专家预测这A、B、C三个团队未来六个月中研究出合格疫苗并用于临床接种的概率分别为![]() ,
,![]() ,
,![]() ,且三个团队是否研究出合格疫苗相互独立.
,且三个团队是否研究出合格疫苗相互独立.
(1)求六个月后A,B两个团队恰有一个研究出合格疫苗并用于临床接种的概率;
(2)设六个月后研究出合格疫苗并用于临床接种的团队个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为4.且过点
的焦距为4.且过点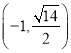 .
.
(1)求椭圆E的方程;
(2)设![]() ,
,![]() ,
,![]() ,过B点且斜率为
,过B点且斜率为![]() 的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线
的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线![]() 相交于点P.证明:
相交于点P.证明:![]() (O为坐标原点).
(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往统计资料,某地车主购买甲种保险的概率为0.4,购买乙种保险但不购买甲种保险的概率为0.2.设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲乙两种保险都不购买的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com