
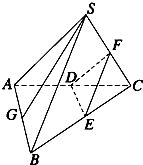
 如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.
如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.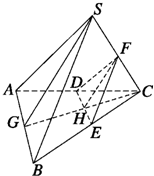 解:根据题意,可得SG与平面DEF的位置关系是SG∥平面DEF,
解:根据题意,可得SG与平面DEF的位置关系是SG∥平面DEF,

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
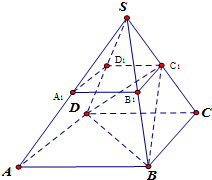 如图所示,正四棱台ABCD-A1B1C1D1是由一个正三棱锥S-ABCD(底面为正方形,顶点在底面上的射影为底面正方形的中心)被平行于底面的平面截所得.已知正四棱台ABCD-A1B1C1D1下底面边长为2,上底面边长为1,高为2.
如图所示,正四棱台ABCD-A1B1C1D1是由一个正三棱锥S-ABCD(底面为正方形,顶点在底面上的射影为底面正方形的中心)被平行于底面的平面截所得.已知正四棱台ABCD-A1B1C1D1下底面边长为2,上底面边长为1,高为2.查看答案和解析>>
科目:高中数学 来源: 题型:
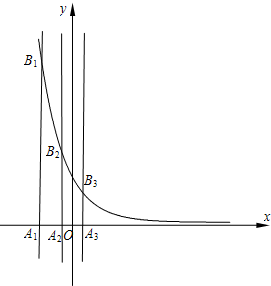 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:013
如图所示,已知正四棱锥
S-ABCD侧棱长为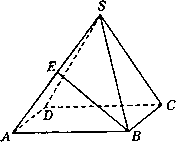
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知正四棱锥S—ABCD侧棱长为![]() ,底面边长为
,底面边长为![]() ,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
A.90° B.60°
C.45° D.30°
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三一轮复习质量检测理科数学 题型:选择题
如图所示,已知正四棱锥S—ABCD侧棱长为 ,底面边长为
,底面边长为 ,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
A.90° B.60° C.45° D.30°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com