
已知函数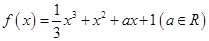 .
.
(1)求函数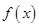 的单调区间;
的单调区间;
(2)当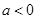 时,试讨论是否存在
时,试讨论是否存在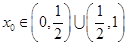 ,使得
,使得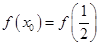 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)先求出导数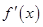 为二次函数,对
为二次函数,对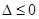 和
和 进行分类讨论,根据导数的正负求出函数
进行分类讨论,根据导数的正负求出函数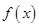 的单调区间;(2)由作差法
的单调区间;(2)由作差法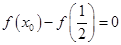 将等式进行因式分解,得到
将等式进行因式分解,得到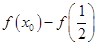
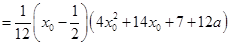 ,于是将问题转化为方程
,于是将问题转化为方程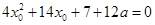 在
在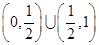 上有解,并求出该方程的两根,并判定其中一根
上有解,并求出该方程的两根,并判定其中一根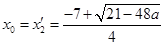 在区间
在区间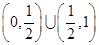 上,并由
上,并由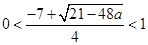 以及
以及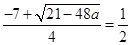 确定满足条件
确定满足条件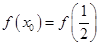 时
时 的取值范围,然后取相应的补集作为满足条件
的取值范围,然后取相应的补集作为满足条件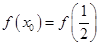 时
时 的取值范围.
的取值范围.
(1)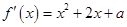 ,方程
,方程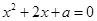 的判别式为
的判别式为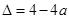 ,
,
①当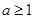 时,
时,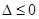 ,则
,则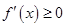 ,此时
,此时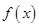 在
在 上是增函数;
上是增函数;
②当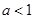 时,方程
时,方程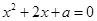 的两根分别为
的两根分别为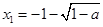 ,
,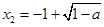 ,
,
解不等式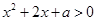 ,解得
,解得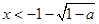 或
或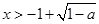 ,
,
解不等式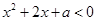 ,解得
,解得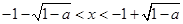 ,
,
此时,函数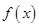 的单调递增区间为
的单调递增区间为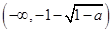 和
和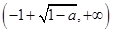 ,
,
单调递减区间为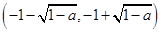 ;
;
综上所述,当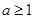 时,函数
时,函数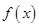 的单调递增区间为
的单调递增区间为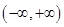 ,
,
当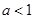 时,函数
时,函数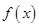 的单调递增区间为
的单调递增区间为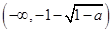 和
和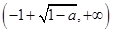 ,
,
单调递减区间为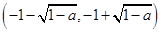 ;
;
(2)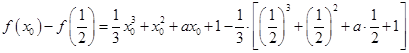

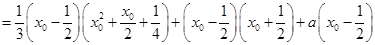
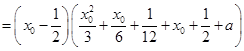
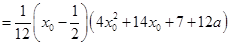 ,
,
若存在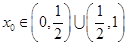 ,使得
,使得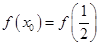 ,
,
必须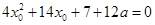 在
在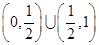 上有解,
上有解,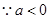 ,
,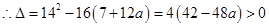 ,
,
方程的两根为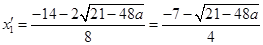 ,
,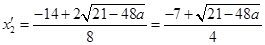 ,
,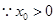 ,
,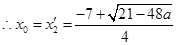 ,
,
依题意,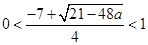 ,即
,即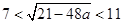 ,
,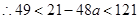 ,即
,即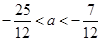 ,
,
又由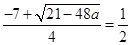 得
得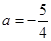 ,
,
故欲使


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且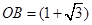 百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设
百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设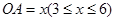 百米,
百米, 百米.
百米.
(1)试将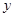 表示成
表示成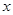 的函数,并求出函数
的函数,并求出函数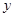 的解析式;
的解析式;
(2)当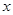 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积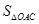 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于定义域为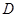 的函数
的函数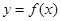 ,若同时满足:
,若同时满足:
① 在
在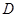 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间[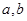 ]
]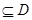 ,使
,使 在
在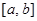 上的值域为
上的值域为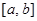 ;
;
那么把函数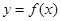 (
(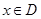 )叫做闭函数.
)叫做闭函数.
(1) 求闭函数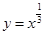 符合条件②的区间
符合条件②的区间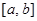 ;
;
(2) 若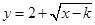 是闭函数,求实数
是闭函数,求实数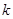 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=-x2+2ex+m-1,g(x)=x+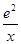 (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的个数.
在(0,1]上解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
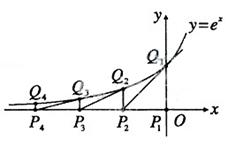
如图,从点P1(0,0)作 轴的垂线交曲线
轴的垂线交曲线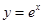 于点
于点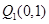 ,曲线在
,曲线在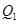 点处的切线与
点处的切线与 轴交于点
轴交于点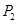 .再从
.再从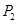 做
做 轴的垂线交曲线于点
轴的垂线交曲线于点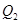 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: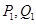 ;
;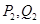 ;…;
;…; ,记
,记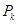 点的坐标为
点的坐标为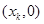 (
(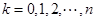 ).
).
(1)试求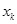 与
与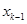 的关系(
的关系(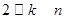 );
);
(2)求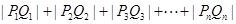 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com