
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(2)当![]() 时,证明:
时,证明:![]() 在
在![]() 上有且仅有一个极大值点和一个极小值点(分别记为
上有且仅有一个极大值点和一个极小值点(分别记为![]() ),且
),且![]() 为定值.
为定值.
【答案】(1)![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .(2)见解析
.(2)见解析
【解析】
(1)当![]() 时,根据函数为奇函数,利用导数研究当
时,根据函数为奇函数,利用导数研究当![]() 时函数的单调性,由此求得函数在
时函数的单调性,由此求得函数在![]() 上的单调性,进而求得最大值和最小值.(2)①将
上的单调性,进而求得最大值和最小值.(2)①将![]() 写成分段函数的形式,当
写成分段函数的形式,当![]() 利用导数求得函数有一个极大值点和一个极小值点,当
利用导数求得函数有一个极大值点和一个极小值点,当![]() 时,函数单调递增,没有极值点.由此证得结论成立. ②根据①的结论,写出关于极值点的韦达定理,计算出
时,函数单调递增,没有极值点.由此证得结论成立. ②根据①的结论,写出关于极值点的韦达定理,计算出 为定值
为定值![]() .
.
(1)当![]() 时,
时,![]() 是奇函数,
是奇函数,
考虑![]() ,
,![]() ,
,
求导得![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,
又根据奇函数的对称性,
可知![]() 在
在![]() 单调递减,
单调递减,![]() 和
和![]() 单调递增
单调递增
![]() ,
,![]() ,
,![]()
所以![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
(2)①当![]() 时,
时,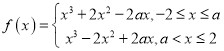
当![]() 时,
时,![]() ,
,![]() ,
,
![]()
![]() ,
,
所以![]() 在
在![]() 有2个根
有2个根![]() ,
,![]() ,
,
其中![]() ,
,![]() ,则
,则![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在
又![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
所以![]() 在
在![]() 上有且仅有一个极大值点
上有且仅有一个极大值点![]() 和一个极小值点
和一个极小值点![]()
②因为![]() 是方程
是方程![]() 的两个根,
的两个根,
所以![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
又![]() ,
,
所以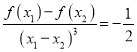 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,侧面![]() 底面ABCD,
底面ABCD,![]() ,底面ABCD是直角梯形,
,底面ABCD是直角梯形,![]()
![]()
![]()
![]() .
.

(1)求证:![]() 平面PBD:
平面PBD:
(2)设E为侧棱PC上异于端点的一点,![]() ,试确定
,试确定![]() 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,在直角梯形![]() 中,AB∥CD,AB⊥BC,CD=2AB=2BC=4,过A点作AE⊥CD,垂足为E,现将ΔADE沿AE折叠,使得DE⊥EC.取AD的中点F,连接BF,CF,EF,如图乙。
中,AB∥CD,AB⊥BC,CD=2AB=2BC=4,过A点作AE⊥CD,垂足为E,现将ΔADE沿AE折叠,使得DE⊥EC.取AD的中点F,连接BF,CF,EF,如图乙。
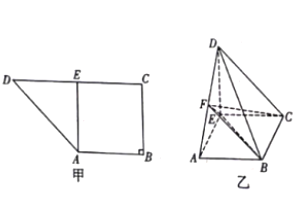
(1)求证:BC⊥平面DEC;
(2)求二面角C-BF-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出三个命题:①直线上有两点到平面的距离相等,则直线平行平面;②夹在两平行平面间的异面直线段的中点的连线平行于这个平面;③过空间一点必有唯一的平面与两异面直线平行.正确的是( )
A. ②③B. ①②C. ①②③D. ②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,证明函数
时,证明函数![]() 是增函数;
是增函数;
(2)是否存在实数![]() ,使得只有唯一的正数
,使得只有唯一的正数![]() ,当
,当![]() 时恒有:
时恒有:![]() ,若这样的实数
,若这样的实数![]() 存在,试求
存在,试求![]() 、
、![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下结论:
①命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题;
有实根”的逆命题为真命题;
④命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是真命题.
”的否命题是真命题.
则其中错误的是__________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com