Question

【题目】化简

（1）

（2）

【答案】(1) ；(2) .

【解析】试题分析：（1）切化弦可得三角函数式的值为－1

（2）结合三角函数的性质可得三角函数式的值为

试题解析：

（1）tan70°cos10°（ tan20°﹣1）

=cot20°cos10°（ ﹣1）

=cot20°cos10°（ ）

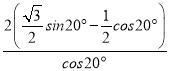=×cos10°×（）

=×cos10°×（）

=×（﹣）

=﹣1

（2）∵（1+tan1°）（1+tan44°）=1+（tan1°+tan44°）+tan1°tan44°

=1+tan（1°+44°）[1﹣tan1°tan44°]+tan1°tan44°=2．

同理可得（1+tan2°）（1+tan43°）

=（1+tan3°）（1+tan42°）

=（1+tan4°）（1+tan41°）=…=2，

故=

点睛：三角函数式的化简要遵循“三看”原则:一看角，这是重要一环，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式 ；二看函数名称，看函数名称之间的差异，从而确定使用的公式，常见的有切化弦；三看结构特征，分析结构特征，可以帮助我们找到变形的方向，如遇到分式要通分等.

【题型】解答题
【结束】
18

【题目】平面内给定三个向量

（1）求

（2）求满足的实数.

（3）若，求实数.

Answer 1

【答案】(1) ；(2) ；(3) .

【解析】试题分析：（1）由向量的线性运算法则即可算出；（2）根据向量相等即可求出m、n的值；

（3）若已知向量=（a，b）、=（c，d），则ad﹣bc=0，计算出即可．

试题解析：

（1）

；

（2）

解之得

（3）又

。