【题目】已知圆C经过A（3，2）、B（1，6），且圆心在直线y=2x上．
（1）求圆C的方程．
（2）若直线l经过点P（﹣1，3）与圆C相切，求直线l的方程．
【答案】
（1）解：∵圆心在直线y=2x上，
故可设圆心C（a，2a），半径为r．
则圆C的标准方程为（x﹣a）2+（y﹣2a）2=r2．
∵圆C经过A（3，2）、B（1，6），
∴ 
．
解得a=2，r= 
．
∴圆C的标准方程为
（x﹣2）2+（y﹣4）2=5．
（2）解：由（1）知，圆C的圆心为C（2，4），半径r= ．
直线l经过点P（﹣1，3），
①若直线斜率不存在，
则直线l：x=﹣1．
圆心C（2，4）到直线l的距离为
d=3＜r= ，故直线与圆相交，不符合题意．
②若直线斜率存在，设斜率为k，
则直线l：y﹣3=k（x+1），
即kx﹣y+k+3=0．
圆心C（2，4）到直线l的距离为
d= 
= 
．
∵直线与圆相切，
∴d=r，即 = ．
∴（3k﹣1）2=5+5k2，
解得k=2或k=- 
．
∴直线l的方程为2x﹣y+5=0或x+2y﹣5=0．
【解析】（1）根据已知设出圆的标准方程，将点A，B的坐标代入标准方程，解方程组即可求出圆心及半径，从而得到圆C的方程．（2）根据已知设出直线方程，利用直线与圆相切的性质d=r即可求出直线斜率k，从而求出直线方程．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知全集U={1，2，3，4，5，6，7，8}，集合A={2，3，5，6}，集合B={1，3，4，6}，则A∪（UB）=（ ）
A.{2，5}
B.{2，5，7，8}
C.{2，3，5，6，7，8}
D.{1，2，3，4，5，6}
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市根据地理位置划分成了南北两区，为调查该市的一种经济作物
（下简称
作物）的生长状况，用简单随机抽样方法从该市调查了 500 处 
作物种植点，其生长状况如表：
其中生长指数的含义是：2 代表“生长良好”，1 代表“生长基本良好”，0 代表“不良好，但仍有收成”，﹣1代表“不良好，绝收”．
（1）估计该市空气质量差的
作物种植点中，不绝收的种植点所占的比例；
（2）能否有 99%的把握认为“该市
作物的种植点是否绝收与所在地域有关”？
（3）根据（2）的结论，能否提供更好的调查方法来估计该市
作物的种植点中，绝收种植点的比例？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
．
⑴ 若曲线
在点
处的切线经过点
，求实数
的值；
⑵ 若函数
在区间
上单调，求实数
的取值范围；
⑶ 设
，若对
， 
，使得
成立，求整数
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设入射光线沿直线y=2x+1射向直线y=x，则被y=x反射后，反射光线所在的直线方程是（ ）
A.x﹣2y﹣1=0
B.x﹣2y+1=0
C.3x﹣2y+1=0
D.x+2y+3=0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥P﹣ABC中，PA=PC=5，PB=4，AB=BC=2 
，∠ACB=30°．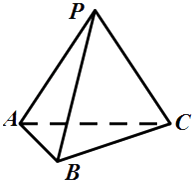 
（1）求证：AC⊥PB；
（2）求三棱锥P﹣ABC的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心在直线y=4x上，且与直线l：x+y﹣2=0相切于点P（1，1）．
（1）求圆的方程；
（2）直线kx﹣y+3=0与该圆相交于A、B两点，若点M在圆上，且有向量 
（O为坐标原点），求实数k．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
