
【题目】已知n为给定的正整数,t为给定的实数,设(t+x)n=a0+a1x+a2x2+…+anxn.
(1)当n=8时.
①若t=1,求a0+a2+a4+a6+a8的值;
②若t=![]() ,求数列{an}中的最大值;
,求数列{an}中的最大值;
(2)若t=![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)①128,②![]() ;(2)
;(2)![]()
【解析】
(1)①设f(x)=(1+x)8=a0+a1x+a2x2+…+a8x8,f(1)=28=a0+a1+a2+…+a8,f(-1)=0=a0-a1+a2-…+a8,a0+a2+a4+a6+a8= [f(1)+ f(-1)] ÷2即可得解;
②![]() ,通过不等式组
,通过不等式组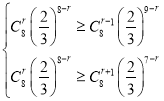 即可得解;
即可得解;
(2)处理![]()
![]()
![]() ,利用二项式定理逆用即可得解.
,利用二项式定理逆用即可得解.
(1)设f(x)=(t+x)n=a0+a1x+a2x2+…+anxn,
当n=8时.
①若t=1,f(x)=(1+x)8=a0+a1x+a2x2+…+a8x8,
f(1)=28=a0+a1+a2+…+a8,f(-1)=0=a0-a1+a2-…+a8,
a0+a2+a4+a6+a8= [f(1)+ f(-1)]÷2=128
②若t=![]() ,(
,(![]() +x)n=a0+a1x+a2x2+…+anxn,
+x)n=a0+a1x+a2x2+…+anxn,
所以![]() ,设第r项最大,则
,设第r项最大,则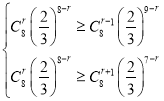 ,
,
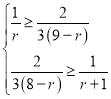 解得
解得![]() ,所以
,所以![]()
数列{an}中的最大值![]()
(2)若t=![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(![]() +x)n=a0+a1x+a2x2+…+anxn,
+x)n=a0+a1x+a2x2+…+anxn,
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]() ,
,
当n=1时也满足,所以![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图①,有一个等腰直角三角板![]() 垂直于平面
垂直于平面![]() ,有一条长为7的细线,其两端分别位于
,有一条长为7的细线,其两端分别位于![]() 处,现用铅笔拉紧细线,在平面
处,现用铅笔拉紧细线,在平面![]() 上移动.
上移动.
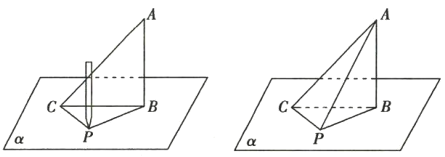
图① 图②
(1)图②中的![]() 的长为多少时,
的长为多少时,![]() 平面
平面![]() ?并给出证明.
?并给出证明.
(2)在(1)的情形下,求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线![]() (a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
(a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
A.若PQ⊥x轴,则△PQF2的周长为![]()
B.连PA交l于D,则必有QD//x轴
C.若PQ中点为M,则必有PQ⊥MF2
D.连PO交双曲线C右支于点N,则必有PQ//NF2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:![]() ,并绘制出频率分布直方图,如图所示.
,并绘制出频率分布直方图,如图所示.
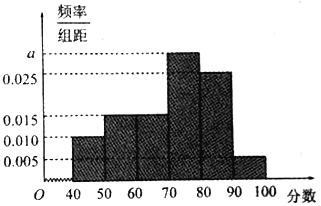
(1)求频率分布直方图中![]() 的值,并估计该市高中学生的平均成绩;
的值,并估计该市高中学生的平均成绩;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 四名学生的考试成绩在区间
四名学生的考试成绩在区间![]() 内,
内,![]() 、
、![]() 两名学生的考试成绩在区间
两名学生的考试成绩在区间![]() 内,现从这6名学生中任选两人参加座谈会,求学生
内,现从这6名学生中任选两人参加座谈会,求学生![]() 、
、![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学组成一个4![]() 100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )
100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有_______.(写出所有正确说法的序号)
①在![]() 中,若
中,若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形;
是锐角三角形;
③在![]() 中,若
中,若![]() ,则
,则![]() ;
;
④若![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,则三点
,则三点![]()
![]()
![]() 共线;
共线;
⑤等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,点
,点![]() 均在函数
均在函数![]() (
(![]() 且
且![]() ,
,![]()
![]() 均为常数)的图象上,则
均为常数)的图象上,则![]() 的值为
的值为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com