
【题目】设z1是虚数,z2=z1![]() 是实数,且﹣1≤z2≤1.
是实数,且﹣1≤z2≤1.
(1)求|z1|的值以及z1的实部的取值范围;
(2)若ω![]() ,求证ω为纯虚数;
,求证ω为纯虚数;
(3)求z2﹣ω2的最小值.
【答案】(1)|z1|=1,取值范围为[![]() ,
,![]() ].(2)见解析(3)1
].(2)见解析(3)1
【解析】
(1)设z1代数形式代入z2,根据z2是实数,求得|z1|,再根据﹣1≤z2≤1,求得z1的实部的取值范围;
(2)根据复数除法法则化简ω,再根据纯虚数概念判断证明;
(3)先化简z2﹣ω2,再利用基本不等式求最小值.
(1)设z1=a+bi,(a,b∈R,且b≠0),
则z2=z1![]() (a+bi)
(a+bi)![]() (a+bi)
(a+bi)![]() (a+bi)
(a+bi)![]() (a
(a![]() )+(b
)+(b![]() )i,
)i,
因为z2是实数,
所以b![]() 0,即b(
0,即b(![]() )=0,
)=0,
因为b≠0,所以a2+b2=1,
即|z1|=1,且z2=2a,
由﹣1≤z2≤1,得﹣1≤2a≤1,解得![]() a
a![]() ,
,
即z1的实部的取值范围为[![]() ,
,![]() ].
].
(2)证明:∵a2+b2=1,
ω![]() ,
,
因为![]() a
a![]() ,b≠0,
,b≠0,
所以ω![]() 为纯虚数.
为纯虚数.
(3)z2﹣ω2=(a![]() )+(b
)+(b![]() )i﹣(
)i﹣(![]() )2,
)2,
=2a+(b﹣b)i![]()
=2a![]()
=2a![]()
![]()
![]()
=1![]()
=1![]()
=1![]()
=1+2(a+1)﹣4![]()
=2(a+1)![]() 3,a+1∈[
3,a+1∈[![]() ,
,![]() ],
],
当2(a+1)![]() 时,即a=0时,z2﹣ω2取最小值1.
时,即a=0时,z2﹣ω2取最小值1.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: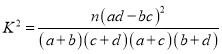 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分別为棱
分別为棱![]() 的中点
的中点

(1)求三棱柱![]() 的体积;
的体积;
(2)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次猜灯谜活动中,共有20道灯谜,两名同学独立竞猜,甲同学猜对了12个,乙同学猜对了8个,假设猜对每道灯谜都是等可能的,试求:
(1)任选一道灯谜,恰有一个人猜对的概率;
(2)任选一道灯谜,甲、乙都没有猜对的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于疫情影响,今年我们学校开展线上教学,高一年级某班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示频率分布直方图,已知从左到右各个小组的频率分别是0.15,0.25,0.35,0.20,0.05,则根据直方图所提供的信息.

(1)这一天上网学习时间在![]() 分钟之间的学生有多少人?
分钟之间的学生有多少人?
(2)这40位同学的线上平均学习时间是多少?
(3)如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间,这样推断是否合理?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知扇形的圆心角是α,半径为R,弧长为l.
(1)若α=75°,R=12 cm,求扇形的弧长l和面积;
(2)若扇形的周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型活动即将举行,为了做好接待工作,组委会招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余人不喜爱运动.
人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男志愿者 | |||
女志愿者 | |||
总计 |
(2)根据列联表判断能否有![]() ℅的把握认为性别与喜爱运动有关?
℅的把握认为性别与喜爱运动有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com