
ЁОЬтФПЁПЮЊМгПьаТФмдДЦћГЕВњвЕЗЂеЙЃЌЭЦНјНкФмМѕХХЃЌЙњМвЙФРјЯћЗбепЙКТђаТФмдДЦћГЕЃЌФГаЃбаОПадбЇЯАаЁзщЃЌДгЦћГЕЪаГЁЩЯЫцЛњбЁШЁСЫ![]() СОДПЕчЖЏГЫгУГЕЃЌИљОнЦфајЪЛРяГЬ
СОДПЕчЖЏГЫгУГЕЃЌИљОнЦфајЪЛРяГЬ![]() ЃЈЕЅДЮГфЕчКѓФмааЪЛЕФзюДѓРяГЬЃЉзїГіСЫЦЕТЪгыЦЕЪ§ЕФЭГМЦБэЃК
ЃЈЕЅДЮГфЕчКѓФмааЪЛЕФзюДѓРяГЬЃЉзїГіСЫЦЕТЪгыЦЕЪ§ЕФЭГМЦБэЃК
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєгУЗжВуГщбљЕФЗНЗЈДгет![]() СОДПЕчЖЏГЫгУГЕжаГщШЁвЛИіШнСПЮЊ6ЕФбљБОЃЌДгИУбљБОжаШЮбЁ2СОЃЌЧѓбЁЕНЕФ2СОГЕајЪЛРяГЬЮЊ
СОДПЕчЖЏГЫгУГЕжаГщШЁвЛИіШнСПЮЊ6ЕФбљБОЃЌДгИУбљБОжаШЮбЁ2СОЃЌЧѓбЁЕНЕФ2СОГЕајЪЛРяГЬЮЊ![]() ЕФИХТЪЃЎ
ЕФИХТЪЃЎ
ЁОД№АИЁПЃЈЂёЃЉ![]() ,
,![]() ,
,![]() ,
,![]() ЃЈЂђЃЉ
ЃЈЂђЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЦЕЪ§ЗжВНБэЃЌПЩЧѓЕУ![]() ЕФжЕЃЌ
ЕФжЕЃЌ
ЃЈ2ЃЉСаОйГібљБОжаШЮбЁ2СОЙВга15жжШЁЗЈЃЌевЕНТњзуЬѕМўЕФЛљБОЪТМўЃЌдйРћгУЙХЕфИХаЭЕФИХТЪЕФЧѓЗЈНтЕУМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈЂёЃЉгЩБэИёПЩжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]()
![]()
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈЂђЃЉЩшЁАДгет![]() СОДПЕчЖЏГЕжаШЮбЁ
СОДПЕчЖЏГЕжаШЮбЁ![]() СОЃЌбЁЕНЕФ
СОЃЌбЁЕНЕФ![]() СОГЕајЪЛРяГЬЮЊ
СОГЕајЪЛРяГЬЮЊ![]() ЁБ
ЁБ
ЮЊЪТМў![]() ЃЌ
ЃЌ
гЩЗжВуГщбљЕУЃКдк![]() жаГщ
жаГщ![]() СОЃЌМЧЮЊ
СОЃЌМЧЮЊ![]() ЃЛдк
ЃЛдк![]() жаГщ
жаГщ![]() СОЃЌМЧЮЊ
СОЃЌМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
дк![]() жаГщ
жаГщ![]() СОЃЌМЧЮЊ
СОЃЌМЧЮЊ![]() ЃЌ
ЃЌ![]() .
.
дђШЮШЁСНСОЙВга![]()
![]()
![]() жжШЁЗЈ
жжШЁЗЈ
ЪТМў![]() га
га![]() жжЧщПі
жжЧщПі
дђ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
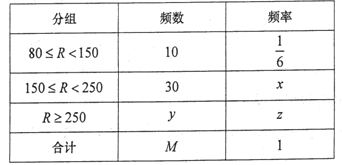
ЁОЬтФПЁПЮЊЕїВщДѓбЇЩњетИіЮЂаХгУЛЇШКЬхжаУПШЫгЕгаЮЂаХШКЕФЪ§СПЃЌЯжДгЮфККЪаДѓбЇЩњжаЫцЛњГщШЁ100ЮЛЭЌбЇНјааСЫГщбљЕїВщЃЌНсЙћШчЯТЃК
ЮЂаХШКЪ§СП | ЦЕЪ§ | ЦЕТЪ |
0жС5Иі | 0 | 0 |
6жС10Иі | 30 | 0.3 |
11жС15Иі | 30 | 0.3 |
16жС20Иі | a | c |
20ИівдЩЯ | 5 | b |
КЯМЦ | 100 | 1 |
ЃЈЂёЃЉЧѓaЃЌbЃЌcЕФжЕЃЛ
ЃЈЂђЃЉвдет100ИіШЫЕФбљБОЪ§ОнЙРМЦЮфККЪаЕФзмЬхЪ§ОнЧввдЦЕТЪЙРМЦИХТЪЃЌШєДгШЋЪаДѓбЇЩњЃЈЪ§СПКмДѓЃЉжаЫцЛњГщШЁ3ШЫЃЌМЧXБэЪОГщЕНЕФЪЧЮЂаХШКИіЪ§ГЌЙ§15ИіЕФШЫЪ§ЃЌЧѓXЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() дк
дк![]() ЩЯЕФзюДѓжЕЃЛ
ЩЯЕФзюДѓжЕЃЛ
ЃЈ2ЃЉСю![]() ЃЌШє
ЃЌШє![]() дкЧјМф
дкЧјМф![]() ЩЯЮЊЕЅЕїЕндіКЏЪ§ЃЌЧѓ
ЩЯЮЊЕЅЕїЕндіКЏЪ§ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкСНЕу
жсНЛгкСНЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌгж
ЃЌгж![]() ЪЧ
ЪЧ![]() ЕФЕМКЏЪ§.Шєе§ГЃЪ§
ЕФЕМКЏЪ§.Шєе§ГЃЪ§![]() ТњзуЬѕМў
ТњзуЬѕМў![]() .ЪдБШНЯ
.ЪдБШНЯ![]() гы0ЕФЙиЯЕЃЌВЂИјГіРэгЩ.
гы0ЕФЙиЯЕЃЌВЂИјГіРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§f(x)ЃНaЃ![]() .
.
(1)Чѓf(0)ЃЛ
(2)ЬНОПf(x)ЕФЕЅЕїадЃЌВЂжЄУїФуЕФНсТлЃЛ
(3)Шєf(x)ЮЊЦцКЏЪ§ЃЌЧѓТњзуf(ax)<f(2)ЕФxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЪ§Са![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФЧА
ЕФЧА![]() ЯюКЭ.жЄУїЃКЖдШЮвт
ЯюКЭ.жЄУїЃКЖдШЮвт![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВCЕФМЋзјБъЗНГЬЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЎШєжБЯп
ЃЎШєжБЯп![]() гыдВCЯрНЛгкВЛЭЌЕФСНЕуPЃЌQЃЎ
гыдВCЯрНЛгкВЛЭЌЕФСНЕуPЃЌQЃЎ
ЃЈЂёЃЉаДГідВCЕФжБНЧзјБъЗНГЬЃЌВЂЧѓдВаФЕФзјБъгыАыОЖЃЛ
ЃЈЂђЃЉШєЯвГЄ|PQ|=4ЃЌЧѓжБЯп![]() ЕФаБТЪЃЎ
ЕФаБТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФСНИіНЙЕуЗжБ№ЮЊ
ЕФСНИіНЙЕуЗжБ№ЮЊ![]() ЃЌРыаФТЪЮЊ
ЃЌРыаФТЪЮЊ![]() .ЩшЙ§Еу
.ЩшЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВ
гыЭждВ![]() ЯрНЛгкВЛЭЌСНЕу
ЯрНЛгкВЛЭЌСНЕу![]() ЃЌ
ЃЌ ![]() жмГЄЮЊ
жмГЄЮЊ![]() .
.
ЃЈЂёЃЉЧѓЭждВCЕФБъзМЗНГЬЃЛ
ЃЈЂђЃЉвбжЊЕу![]() ЃЌжЄУїЃКЕБжБЯп
ЃЌжЄУїЃКЕБжБЯп![]() БфЛЏЪБЃЌзмгаTAгы
БфЛЏЪБЃЌзмгаTAгы![]() ЕФаБТЪжЎКЭЮЊЖЈжЕЃЎ
ЕФаБТЪжЎКЭЮЊЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=![]() +xдкx=1ДІЕФЧаЯпЗНГЬЮЊ2xЉy+b=0ЃЎ
+xдкx=1ДІЕФЧаЯпЗНГЬЮЊ2xЉy+b=0ЃЎ
ЃЈЂёЃЉЧѓЪЕЪ§aЃЌbЕФжЕЃЛ
ЃЈЂђЃЉШєКЏЪ§gЃЈxЃЉ=fЃЈxЃЉ+![]() x2ЉkxЃЌЧвgЃЈxЃЉЪЧЦфЖЈвхгђЩЯЕФдіКЏЪ§ЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
x2ЉkxЃЌЧвgЃЈxЃЉЪЧЦфЖЈвхгђЩЯЕФдіКЏЪ§ЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊСНдВC1ЃКx2ЃЋy2Ѓ2xЃ6yЃ1ЃН0КЭC2ЃКx2ЃЋy2Ѓ10xЃ12yЃЋ45ЃН0.
(1)ЧѓжЄЃКдВC1КЭдВC2ЯрНЛЃЛ
(2)ЧѓдВC1КЭдВC2ЕФЙЋЙВЯвЫљдкжБЯпЕФЗНГЬКЭЙЋЙВЯвГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com