
| A. | $\frac{5}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{10}}{2}$ |
分析 通过双曲线的特点知原点O为两焦点的中点,利用中位线的性质,求出PF′的长度及判断出PF′垂直于PF,通过勾股定理得到a,c的关系,进而求出双曲线的离心率.
解答 解:如图,记右焦点为F′,则O为FF′的中点,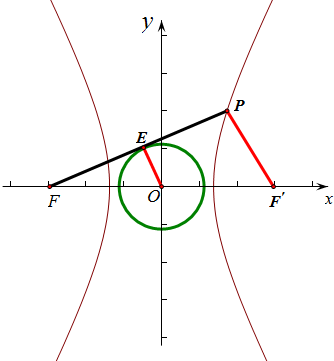
∵E为PF的中点,
∴OE为△FF′P的中位线,
∴PF′=2OE=a,
∵E为切点,
∴OE⊥PF,
∴PF′⊥PF,
∵点P在双曲线上,
∴PF-PF′=2a,
∴PF=PF′+2a=3a,
在Rt△PFF′中,有:PF2+PF′2=FF′2,
∴9a2+a2=4c2,即10a2=4c2,
∴离心率e=$\frac{c}{a}$=$\frac{\sqrt{10}}{2}$,
故选:D.
点评 本题主要考查双曲线的简单性质、圆的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,在圆锥曲线中,求离心率关键就是求三参数a,b,c的关系,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
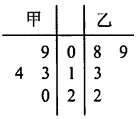 甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )
甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )| A. | v1>v2,s1>s2 | B. | v1<v2,s1>s2 | C. | v1>v2,s1<s2 | D. | v1<v2,s1<s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分数 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 20 | 10 | 40 | 10 | 20 |
| A. | 3 | B. | 2.5 | C. | 3.5 | D. | 2.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
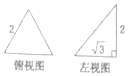 已知三棱锥的俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一条直角边为2的直角三角形,则该三棱锥的主视图可能为( )
已知三棱锥的俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一条直角边为2的直角三角形,则该三棱锥的主视图可能为( )| A. | 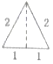 | B. |  | C. | 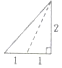 | D. | 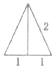 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com