
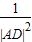 =
=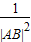 +
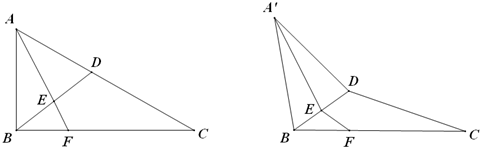
+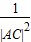 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出哪些结论?至少写出两个结论.
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出哪些结论?至少写出两个结论.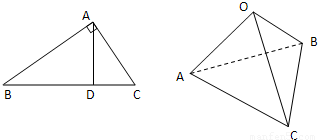
 =
=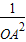 +
+ +
+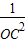 (H为△ABC的重心)
(H为△ABC的重心)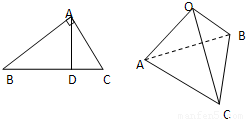
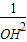 =
=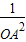 +
+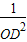
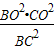 又∵BC2=BO2+CO2
又∵BC2=BO2+CO2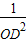 =
=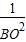 +
+ ②由①②得:
②由①②得: =
= +
+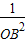 +
+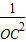

 ab S△OBC=
ab S△OBC= bc S△OAC=
bc S△OAC= ac
ac  BC•AD
BC•AD ( a2 b2+b2 c2+a2 c2)=
( a2 b2+b2 c2+a2 c2)= a2(b2+c2)+
a2(b2+c2)+ b2 c2…①
b2 c2…① (b2+c2)•AD2=
(b2+c2)•AD2= BC2•AD2=S△ABC2
BC2•AD2=S△ABC2

科目:高中数学 来源: 题型:
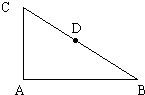 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,|AB|=2
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,|AB|=2| 3 |
| 1 |
| 2 |
| DM |
| DN |
| MN |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
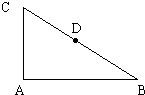 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,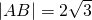 ,
,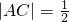 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C.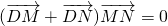 ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com