
【题目】如图,在四棱锥![]() 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上且
上且![]() 平面
平面![]() ,
,![]() 在
在![]() 延长线上,
延长线上,![]() ,交
,交![]() 于
于![]() ,且
,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱中ABC—A1B1C1,ABAC,AB=3,AC=4,B1CAC1.

(1)求AA1的长;
(2)试判断在侧棱BB1上是否存在点P,使得直线PC与平面AA1C1C所成角和二面角B—A1C—A的大小相等,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时,![]() 的面积为
的面积为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经点
经点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,设直线
,设直线![]() 过椭圆
过椭圆![]() 的上顶点和右焦点,坐标原点
的上顶点和右焦点,坐标原点![]() 到直线
到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 且斜率不为零的直线交椭圆
且斜率不为零的直线交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之积为非零的常数?若存在,求出定点
的斜率之积为非零的常数?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面α∩平面β=l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )

A.若AB![]() CD,则MN
CD,则MN![]() l
l
B.若M,N重合,则AC![]() l
l
C.若AB与CD相交,且AC![]() l,则BD可以与l相交
l,则BD可以与l相交
D.若AB与CD是异面直线,则MN不可能与l平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中总务处的老师要购买学校教学用的粉笔,并且有非常明确的判断一盒粉笔是“优质产品”和“非优质产品”的方法.某品牌的粉笔整箱出售,每箱共有20盒,根据以往的经验,其中会有某些盒的粉笔为非优质产品,其余的都为优质产品.并且每箱含有0,1,2盒非优质产品粉笔的概率为0.7,0.2和0.1.为了购买该品牌的粉笔,校总务主任设计了一种购买的方案:欲买一箱粉笔,随机查看该箱的4盒粉笔,如果没有非优质产品,则购买,否则不购买.设“买下所查看的一箱粉笔”为事件![]() ,“箱中有
,“箱中有![]() 件非优质产品”为事件
件非优质产品”为事件![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)随机查看该品牌粉笔某一箱中的四盒,设![]() 为非优质产品的盒数,求
为非优质产品的盒数,求![]() 的分布列及期望;
的分布列及期望;
(3)若购买100箱该品牌粉笔,如果按照主任所设计方案购买的粉笔中,箱中每盒粉笔都是优质产品的箱数的期望比随机购买的箱中每盒粉笔都是优质产品的箱数的期望大10,则所设计的方案有效.讨论该方案是否有效.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,
中,底面ABCD为矩形,![]() ,
,![]() ,侧面SAD是以AD为斜边的等腰直角三角形,且平面
,侧面SAD是以AD为斜边的等腰直角三角形,且平面![]() 平面ABCD,M,N分别为AD,SC的中点.
平面ABCD,M,N分别为AD,SC的中点.
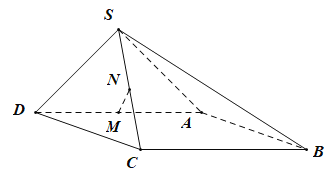
(1)求证:![]() 平面SAB.
平面SAB.
(2)求直线BN与平面SAB所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com