
【题目】已知函数f(x)=2sin(ωx+ ![]() )的图象与x轴交点的横坐标,依次构成一个公差为
)的图象与x轴交点的横坐标,依次构成一个公差为 ![]() 的等差数列,把函数f(x)的图象沿x轴向左平移
的等差数列,把函数f(x)的图象沿x轴向左平移 ![]() 个单位,得到函数g(x)的图象,则( )
个单位,得到函数g(x)的图象,则( )
A.g(x)是奇函数
B.g(x)的图象关于直线x=﹣ ![]() 对称
对称
C.g(x)在[ ![]() ,
, ![]() ]上的增函数
]上的增函数
D.当x∈[ ![]() ,
, ![]() ]时,g(x)的值域是[﹣2,1]
]时,g(x)的值域是[﹣2,1]
【答案】D
【解析】解:函数f(x)=2sin(ωx+ ![]() )的图象与x轴交点的横坐标, 依次构成一个公差为
)的图象与x轴交点的横坐标, 依次构成一个公差为 ![]() 的等差数列,
的等差数列,
∴ ![]() =
= ![]() =
= ![]() ,∴ω=2,f(x)=2sin(2x+
,∴ω=2,f(x)=2sin(2x+ ![]() ).
).
把函数f(x)的图象沿x轴向左平移 ![]() 个单位,
个单位,
得到函数g(x)=2sin[2(x+ ![]() )+
)+ ![]() ]=2sin(2x+
]=2sin(2x+ ![]() )=2cos2x的图象,
)=2cos2x的图象,
故g(x)是偶函数,故排除A;
当x=﹣ ![]() 时,g(x)=0,故g(x)的图象不关于直线x=﹣
时,g(x)=0,故g(x)的图象不关于直线x=﹣ ![]() 对称,故排除B;
对称,故排除B;
在[ ![]() ,
, ![]() ]上,2x∈[
]上,2x∈[ ![]() ,π],故g(x)在[
,π],故g(x)在[ ![]() ,
, ![]() ]上的减函数,故排除C;
]上的减函数,故排除C;
当x∈[ ![]() ,
, ![]() ]时,2x∈[
]时,2x∈[ ![]() ,
, ![]() ],当2x=π时,g(x)=2cos2x取得最小值为﹣2,
],当2x=π时,g(x)=2cos2x取得最小值为﹣2,
当2x= ![]() 时,g(x)=2cos2x取得最大值为1,故函数 g(x)的值域为[﹣2,1],
时,g(x)=2cos2x取得最大值为1,故函数 g(x)的值域为[﹣2,1],
故选:D.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】己知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方f(x)程f(x)+2=f( ![]() )的实数x为 ( )
)的实数x为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=xex(e为自然对数的底数),g(x)=(x+1)2 .
(I)记 ![]() ,讨论函F(x)单调性;
,讨论函F(x)单调性;
(II)令G(x)=af(x)+g(x)(a∈R),若函数G(x)有两个零点.
(i)求参数a的取值范围;
(ii)设x1 , x2是G(x)的两个零点,证明x1+x2+2<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1 , ∠BAA1=∠BAC=60°,点O是线段AB的中点. (Ⅰ)证明:BC1∥平面OA1C;
(Ⅱ)若AB=2,A1C= ![]() ,求二面角A﹣BC﹣A1的余弦值.
,求二面角A﹣BC﹣A1的余弦值.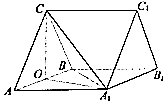
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.函数y=sinx,x∈[0,2π]是奇函数
B.函数y=2sin( ![]() ﹣2x)在区间[﹣
﹣2x)在区间[﹣ ![]() ]上单调递减
]上单调递减
C.函数y=2sin( ![]() -2x)﹣cos(
-2x)﹣cos( ![]() +2x)(x∈R)的一条对称轴方程是x=
+2x)(x∈R)的一条对称轴方程是x= ![]()
D.函数y=sinπx?cosπx的最小正周期为2,且它的最大值为1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD= ![]() AD,AE⊥PC于点E,EF∥CD,交PD于点F (Ⅰ)证明:平面ADE⊥平面PBC
AD,AE⊥PC于点E,EF∥CD,交PD于点F (Ⅰ)证明:平面ADE⊥平面PBC
(Ⅱ)求二面角D﹣AE﹣F的余弦值.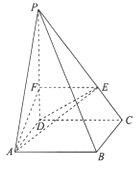
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|2x+a|,a∈R. (Ⅰ)当a=1时,解不等式f(x)≥5;
(Ⅱ)若存在x0满足f(x0)+|x0﹣2|<3,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com