
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
【答案】(1)f(x)=![]() x(x≥0),g(x)=
x(x≥0),g(x)=![]()
![]() (x≥0);(2)投资A类为16万元,投资B类为4万,最大3万元.
(x≥0);(2)投资A类为16万元,投资B类为4万,最大3万元.
【解析】
试题分析:(1)由投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;
(2)由(1)的结论,我们设设投资债券类产品x万元,则股票类投资为20-x万元.这时可以构造出一个关于收益y的函数,然后利用求函数最大值的方法进行求解.
试题解析:(1)设![]() 两类产品的收益与投资额的函数分别为f(x)=k1x,g(x)=k2
两类产品的收益与投资额的函数分别为f(x)=k1x,g(x)=k2![]() .
.
由已知得f(1)=![]() =k1,g(1)=
=k1,g(1)=![]() =k2,所以f(x)=
=k2,所以f(x)=![]() x(x≥0),g(x)=
x(x≥0),g(x)=![]()
![]() (x≥0).
(x≥0).
(2)设投资![]() 类产品为x万元,则投资
类产品为x万元,则投资![]() 类产品为(20-x)万元.
类产品为(20-x)万元.
依题意得y=f(x)+g(20-x)=![]() +
+![]()
![]() (0≤x≤20).
(0≤x≤20).
令t=![]() (0≤t≤2
(0≤t≤2![]() ),则y=
),则y=![]() +
+![]() t=-
t=-![]() (t-2)2+3,
(t-2)2+3,
所以当t=2,即x=16时,收益最大,ymax=3万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】画出下列函数的图像,并根据图像说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数。
(1)y=x2-5x-6; (2)y=|4-x2|.
查看答案和解析>>
科目:高中数学 来源: 题型:
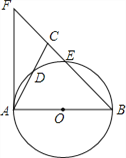
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若![]() ,CE∶EB=1∶4,求CE的长.
,CE∶EB=1∶4,求CE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() ,
,![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数茎叶图如下:
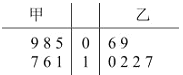
(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数![]() ,使得原
,使得原![]() 上有四点到直线
上有四点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() 的对角线交于点
的对角线交于点![]() ,边
,边![]() 所在直线的方程为
所在直线的方程为![]() ,点
,点![]() 在边
在边![]() 所在的直线上.
所在的直线上.
(1)求矩形![]() 的外接圆的方程;
的外接圆的方程;
(2)已知直线![]() (
(![]() ),求证:直线
),求证:直线![]() 与矩形
与矩形![]() 的外接圆恒相交,并求出相交的弦长最短时的直线
的外接圆恒相交,并求出相交的弦长最短时的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
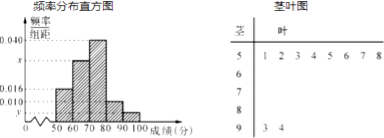
【题目】吉安一中举行了一次“环保知识竞赛”活动,为了解本了次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计. 按照
)进行统计. 按照 ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛学生成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到市政广场参加环保知识宣传的志愿者活动,设
名同学到市政广场参加环保知识宣传的志愿者活动,设![]() 表示所抽取的
表示所抽取的![]() 名同学中得分在
名同学中得分在![]() 的学生人数,求
的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com