
【题目】如图,在底面为矩形的四棱锥![]() 中,
中, ![]() .
.
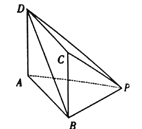
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且x>0时,f(x)=1+( ![]() )x
)x
(1)求函数f(x)的解析式;
(2)画出函数f(x)的草图; 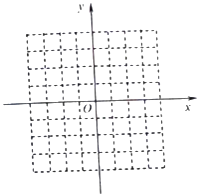
(3)利用图象直接写出函数f(x)的单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
)x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
(1)求集合A∩B,(UB)∪A;
(2)若A∪C=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.
(1)求f(x)的最小值g(a)的解析式;
(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R均成立,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求广告费支出x与销售额y回归直线方程 ![]() =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b= 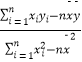 ,
, ![]()
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
, ![]() 为垂足,点
为垂足,点![]() 满足
满足![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若![]() 两点分别为椭圆
两点分别为椭圆![]() 的左右顶点,
的左右顶点, ![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com