
【题目】如图,在三棱柱![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求证:直线![]()
![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)设![]() 与
与![]() 交于点,
交于点, ![]() 连接
连接![]() ,
, ![]() .由几何关系可证得四边形
.由几何关系可证得四边形![]() 是平行四边形,则
是平行四边形,则![]() .由线面平行的判断定理可得直线
.由线面平行的判断定理可得直线![]() 平面
平面![]() .
.
(2)由题意可得![]() 是菱形,则
是菱形,则![]() ,由等腰三角形三线合一可得
,由等腰三角形三线合一可得![]() ,结合
,结合![]() ,可得
,可得![]() ,则
,则![]() ,
, ![]() ,利用线面垂直的判断定理可得直线
,利用线面垂直的判断定理可得直线![]() 平面
平面![]() .
.
试题解析:
(1)如图,设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
, ![]() .
.
因为四边形![]() 是平行四边形,
是平行四边形,
所以是![]() 是
是![]() 的中点.
的中点.
又![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
, ![]() .
.
又因为![]() 是
是![]() 的中点,
的中点,
所以![]() ,
, ![]() .
.
所以![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.

(2)因为![]() ,
,
所以平行四边形![]() 是菱形,所以
是菱形,所以![]() ,
,
因为![]() ,
, ![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
所以![]() .故
.故![]() ,即
,即![]() .
.
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.下图是赵爽弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2![]() 勾
勾![]() 股
股![]() (股
(股![]() 勾)2
勾)2![]() 4
4![]() 朱实
朱实![]() 黄实
黄实![]() 弦实,化简得勾2
弦实,化简得勾2![]() 股2
股2![]() 弦2.若图中勾股形的勾股比为
弦2.若图中勾股形的勾股比为![]() ,若向弦图内随机抛掷2000颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,若向弦图内随机抛掷2000颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆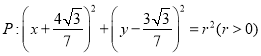 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
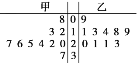
A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为![]() ,
, ![]() ,
, ![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织了数学学科考试,随机抽取50名学生的成绩并制成频率分布直方图如图所示.

(1)求m的值,并估计高一年级所有学生数学成绩在![]() 分的学生所占的百分比;
分的学生所占的百分比;
(2)分别估计这50名学生数学成绩的平均数和中位数.(同一组中的数据以该组区间的中点值作代表,结果精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com