Question

设b和c分别是先后抛掷一枚骰子得到的点数，用随机变量ξ表示方程x²+bx+c=0实根的个数（重根按一个计）．
（Ⅰ）求方程x²+bx+c=0有实根的概率；
（Ⅱ）求ξ的分布列和数学期望；

Answer 1

分析：（1）由题意知本题是一个古典概型，试验发生包含的所有事件根据分步计数原理知是36，满足条件的事件是方程x²+bx+c=0有实根包括有一个实根，有两个实根，这两种结果是互斥的，根据互斥事件的概率公式得到结果．
（2）由题意知实根的个数只有三种结果，0、1、2，根据上一问的计算可以写出当变量取值时对应的概率，写出分布列，算出期望．

解答：解：（Ⅰ）由题意知：设基本事件空间为Ω，
记“方程x²+bx+c=0没有实根”为事件A，
“方程x²+bx+c=0有且仅有一个实根”为事件B，
“方程x²+bx+c=0有两个相异实数”为事件C
则Ω={（b，c）|b，c=1，2，3，4，5，6}
Ω是的基本事件总数为36个，
A={（b，c）|b²-4c＜0，b，c=1，2，3，4，5，6}，A中的基本事件总数为17个；
B={（b，c）|b²-4c=0，b，c=1，2，3，4，5，6}，B中的基本事件总数为2个；
C={（b，c）|b²-4c＞0，b，c=1，2，3，4，5，6}，C中的基本事件总数为17个；
又因为B，C是互斥事件，
∴所求概率P=P（B）+P（C）=

2

36

+

17

36

=

19

36

．
（Ⅱ）由题意，ξ的可能取值为0，1，2，则
P（ξ=0）=

17

36

，
P（ξ=1）=

1

18

P（ξ=2）=

17

36

∴ξ的分布列为：

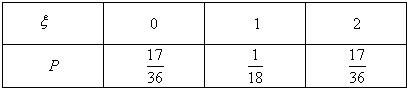
∴ξ的数学期望Eξ=0×

17

36

+1×

1

18

+2×

17

36

=1

点评：本题主要考查离散型随机变量的分布列和古典概型，古典概型要求能够列举出所有事件和发生事件的个数，本题可以列举出所有事件，概率问题同其他的知识点结合在一起，实际上是以概率问题为载体，主要考查的是另一个知识点，本题考查一元二次方程的解．