
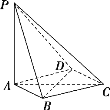
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(1)求证:BD⊥平面PAC;
(2)若PA=4,求平面PBC与平面PDC所成角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)通过证明BD⊥AC和BD⊥PA,可证得结论;
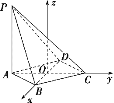
(2)以BD与AC的交点O为坐标原点,OB,OC所在直线为x轴,y轴,过点O且垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系,分别计算平面PBC的一个法向量为n1,平面PDC的一个法向量为n2,利用向量夹角公式可得解.
(1)证明:因为底面ABCD是菱形,所以BD⊥AC.
又PA⊥平面ABCD,
所以BD⊥PA.又PA∩AC=A,所以BD⊥平面PAC.
(2)以BD与AC的交点O为坐标原点,OB,OC所在直线为x轴,y轴,过点O且垂直于平面ABCD的直线为z轴,建立如图所示的空间直角坐标系.
由已知可得,AO=OC=![]() ,OD=OB=1,
,OD=OB=1,
所以P(0,-![]() ,4),B(1,0,0),C(0,
,4),B(1,0,0),C(0,![]() ,0),D(-1,0,0),
,0),D(-1,0,0),
![]() (0,2
(0,2![]() ,-4),
,-4),![]() =(-1,
=(-1,![]() ,0),
,0),![]() =(-1,-
=(-1,-![]() ,0).
,0).
设平面PBC的一个法向量为n1=(x1,y1,z1),平面PDC的一个法向量为n2=(x2,y2,z2),
由可得![]() 令x1=
令x1=![]() ,可得n1=
,可得n1=![]() .
.
同理,由可得n2=![]() ,
,
所以cos〈n1,n2〉=![]() =-
=-![]() ,所以平面PBC与平面PDC所成角的余弦值为
,所以平面PBC与平面PDC所成角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间情况,某经销化妆品的微商在一广场随机采访男性、女性微信用户各50名.其中每天玩微信时间超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如表:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从参与调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽选取的5人中再随机抽取3人赠送价值200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列及数学期望及方差.
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若正数![]() 是等差数列,则
是等差数列,则![]() 是等比数列
是等比数列
B.若正数是![]() 等比数列,则
等比数列,则![]() 是等差数列
是等差数列
C.若正数是![]() 等差数列,则
等差数列,则![]() 是等比数列
是等比数列
D.若正数是![]() 等比数列,则是
等比数列,则是![]() 等差数列
等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探究函数![]() 的图像时,列表如下:
的图像时,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
观察表中y值随x值的变化情况,完成以下的问题:
(1)函数![]() 的递减区间是 ,递增区间是 ;
的递减区间是 ,递增区间是 ;
(2)若对任意的![]() 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过原点,且在
的图象过原点,且在![]() 处取得极值,直线
处取得极值,直线![]() 与曲线
与曲线![]() 在原点处的切线互相垂直.
在原点处的切线互相垂直.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若对任意实数的![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子产品的不断更新完善,更多的电子产品逐步走入大家的世界,给大家带来了丰富多彩的生活,但也带来了一些负面的影响,某公司随即抽取![]() 人对某电子产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对某电子产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的年龄层次以及意见进行了分类,得到的数据如下表所示:
人中的年龄层次以及意见进行了分类,得到的数据如下表所示:
|
| 总计 | |
认为某电子产品对生活有益 |
|
|
|
认为某电子产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为电子产品的态度与年龄有关系?
的前提下,认为电子产品的态度与年龄有关系?
(2)为了答谢参与问卷调查的人员,该公司对参与本次问卷调查的人员进行抽奖活动,奖金额以及发放的概率如下:
奖金额 |
|
|
|
概率 |
|
|
|
现在甲、乙两人参与了抽奖活动,记两人获得的奖金总金额为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1和图2中所有的正方形都全等,图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学参加比赛,只有其中三位获奖.甲说:“乙或丙未获奖”;乙说:“甲、丙都获奖”;丙说:“我未获奖”;丁说:“乙获奖”.四位同学的话恰有两句是对的,则( )
A. 甲和乙不可能同时获奖 B. 丙和丁不可能同时获奖
C. 乙和丁不可能同时获奖 D. 丁和甲不可能同时获奖
【答案】C
【解析】若甲乙丙同时获奖,则甲丙的话错,乙丁的话对;符合题意;
若甲乙丁同时获奖,则乙的话错,甲丙丁的话对;不合题意;
若甲丙丁同时获奖,则丙丁的话错,甲乙的话对;符合题意;;
若丙乙丁同时获奖,则甲乙丙的话错,丁的话对;不合题意;
因此乙和丁不可能同时获奖,选C.
【题型】单选题
【结束】
12
【题目】已知当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有唯一实数解,则
有唯一实数解,则![]() 值所在的范围是( )
值所在的范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com