练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】要测量电视塔AB的高度，在C点测得塔顶的仰角是45°，在D点测得塔顶的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，则电视塔的高度是（ ）
    A.30m
    B.40m
    C. m
    D. m

    【答案】B
    【解析】解：由题题意，设AB=x，则BD= x，BC=x 在△DBC中，∠BCD=120°，CD=40，
    ∴根据余弦定理，得BD2=BC2+CD2﹣2BCCDcos∠DCB
    即：（ x）2=（40）2+x2﹣2×40xcos120°
    整理得x2﹣20x﹣800=0，解之得x=40或x=﹣20（舍）
    即所求电视塔的高度为40米．
    故选B．

    设出AB=x，进而根据题意将BD、DC用x来表示，然后在△DBC中利用余弦定理建立方程求得x，即可得到电视塔的高度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=2， cos2B+5cosB﹣ =0，且点D在线段BC上．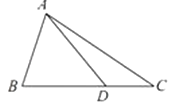
    （1）若∠ADC= ，求AD的长；
    （2）若BD=2DC， =4 ，求△ABD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx﹣ax+ ，且f（x）+f（ ）=0，其中a，b为常数．
    （1）若函数f（x）的图象在x=1的切线经过点（2，5），求函数的解析式；
    （2）已知0＜a＜1，求证：f（ ）＞0；
    （3）当f（x）存在三个不同的零点时，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|x﹣1|﹣|2x+1|的最大值为m．
    （Ⅰ）作出函数f（x）的图象；
    （Ⅱ）若a2+2c2+3b2=m，求ab+2bc的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣alnx（a＞0）的最小值是1．
    （Ⅰ）求a；
    （Ⅱ）若关于x的方程f2（x）ex﹣6mf（x）+9me﹣x=0在区间[1，+∞）有唯一的实根，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 上两个不同的点A，B关于直线y=mx+ 对称．
    （1）求实数m的取值范围；
    （2）求△AOB面积的最大值（O为坐标原点）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且b，c是关于x的一元二次方程x2+mx﹣a2+b2+c2=0的两根．
    （1）求角A的大小；
    （2）已知a= ，设B=θ，△ABC的面积为y，求y=f（θ）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜ ）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到的图象关于点（ ，﹣1）对称，则m的最小值是（ ）
    A.
    B.
    C. π
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：

    周销售量

    2

    3

    4

    频数

    20

    50

    30


    （1）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；
    （2）已知每吨该商品的销售利润为2千元，ξ表示该种商品两周销售利润的和（单位：千元），若以上述频率作为概率，且各周的销售量相互独立，求ξ的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案