
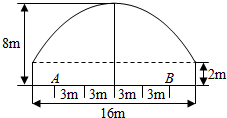
 有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).
有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示). 分析 根据题意,适当建立坐标系,如:以抛物线的对称轴为y轴,路面为x轴,可确定抛物线的顶点坐标及与x轴右交点坐标,设抛物线的顶点式,把右交点坐标代入,可求抛物线解析式;规定车辆必须在中心线右侧距道路边缘2米这一范围内行驶,即此时车子的右边横坐标为6,代入解析式求此时的纵坐标,回答题目问题.
解答  解:如图,以抛物线的对称轴为y轴,路面为x轴,建立坐标系,
解:如图,以抛物线的对称轴为y轴,路面为x轴,建立坐标系,
由已知可得,抛物线顶点坐标为(0,6),与x轴的一个交点(8,0),
设抛物线解析式为y=ax2+6,
把(8,0)代入解析式,
得a=-$\frac{3}{32}$,
所以,抛物线解析式为y=-$\frac{3}{32}$x2+6,
当x=6时,y≈4.3,
∴慢车道的限制高度为 4.3米.
点评 实际问题中的抛物线问题,一般要建立直角坐标系解决,适当建立坐标系可使抛物线解析式形式上简单,便于利用题目的已知条件求解析式.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
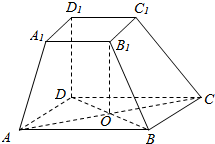 在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.
在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com