B
分析:令n=1,得到第1项与第2项的积为16,记作①,令n=2,得到第2项与第3项的积为256,记作②,然后利用②÷①,利用等比数列的通项公式得到关于q的方程,求出方程的解即可得到q的值,然后把q的值代入经过检验得到满足题意的q的值即可.
解答:当n=1时,a
1a
2=16①;当n=2时,a
2a
3=256②,
②÷①得:
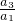
=16,即q
2=16,解得q=4或q=-4,
当q=-4时,由①得:a
12×(-4)=16,即a
12=-4,无解,所以q=-4舍去,
则公比q=4.
故选B
点评:此题考查学生掌握等比数列的性质,灵活运用等比数列的通项公式化简求值,是一道基础题.学生在求出q的值后,要经过判断得到满足题意的q的值,即把q=-4舍去.

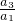 =16,即q2=16,解得q=4或q=-4,
=16,即q2=16,解得q=4或q=-4,
