
【题目】用![]() 组成没有重复数字的五位数abcde,其中随机取一个五位数,满足条件
组成没有重复数字的五位数abcde,其中随机取一个五位数,满足条件![]() 的概率为________.
的概率为________.
【答案】![]()
【解析】
五位数有![]() 个,可用分类讨论思想求得满足条件
个,可用分类讨论思想求得满足条件![]() 的五位数的个数.由四个绝对值中最大值分别为3,2,1分类可得,然后可计算概率.
的五位数的个数.由四个绝对值中最大值分别为3,2,1分类可得,然后可计算概率.
没有重复数字的五位数有![]() 个,
个,
![]() ,由于四个绝对值最小为1,最大的不可能为4,
,由于四个绝对值最小为1,最大的不可能为4,
若最大值为3的五位数有12543,34521,54123,32145共4个,
四个绝对值最大为2,只有1个是2时,五位数有:21345,12354,54312,45321共4个,
四绝对值中两个为2,两个为1时,这样的五位数有:13245,31245,21345,54231,54213,45312,53421,35421,12435,12453共10个,
四个绝对值都等于1的五位数有:12345,54321共2个,
综上满足题意的五位数有4+4+10+2=20个,
∴所求概率为![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,设
,设![]() 为线段
为线段![]() 的中点.则在
的中点.则在![]() 翻折过程中,给出如下结论:
翻折过程中,给出如下结论:
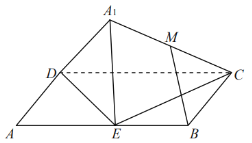
①当![]() 不在平面
不在平面![]() 内时,
内时,![]() 平面
平面![]() ;
;
②存在某个位置,使得![]() ;
;
③线段![]() 的长是定值;
的长是定值;
④当三棱锥![]() 体积最大时,其外接球的表面积为
体积最大时,其外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.(请将所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆
在圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 上的点
上的点![]() 满足
满足![]() .过点
.过点![]() 作直线
作直线![]() 垂直于线段
垂直于线段![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)证明:![]() 恒过定点;
恒过定点;
(ⅱ)设线段![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .若将曲线
.若将曲线![]() 上的所有点的横坐标缩小到原来的一半,纵坐标伸长到原来的
上的所有点的横坐标缩小到原来的一半,纵坐标伸长到原来的![]() 倍,得曲线
倍,得曲线![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() , 直线
, 直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某植物学家培养出一种观赏性植物,会开出红花或黄花,已知该植物第一代开红花和黄花的概率都是![]() ,从第二代开始,若上一代开红花,则这一代开红花的概率是
,从第二代开始,若上一代开红花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() ;若上一代开黄花,则这一代开红花的概率是
;若上一代开黄花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() .记第n代开红花的概率为
.记第n代开红花的概率为![]() ,第n代开黄花的概率为
,第n代开黄花的概率为![]() .
.
(1)求![]() ;
;
(2)①证明:数列![]() 为等比数列;
为等比数列;
②第![]() 代开哪种颜色花的概率更大?
代开哪种颜色花的概率更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的五面体中,![]() 是正方形,
是正方形,![]() 是等腰梯形,且平面
是等腰梯形,且平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,记
上,记![]() ,
,![]() 是线段
是线段![]() 上的动点. 当
上的动点. 当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积为定值?证明此时二面角
的体积为定值?证明此时二面角![]() 为定值,并求出其余弦值.
为定值,并求出其余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省为迎接新高考,拟先对考生某选考学科的实际得分进行等级赋分,再按赋分后的分数从高分到低分划A、B、C、D、E五个等级,考生实际得分经赋分后的分数在到1之间.在等级赋分科学性论证时,对过去一年全省高考考生的该学科成绩重新赋分后进行分析,随机抽取2000名学生的该学科赋分后的成绩,得到如下频率分布直方图:(不考虑缺考考生的试卷)
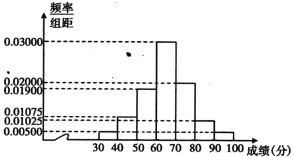
附:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974,![]() =14.59,∑(xi-
=14.59,∑(xi-![]() )2pi=213
)2pi=213
(1)求这2000名考生赋分后该学科的平均![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由频率分布直方图可以认为,学生经过赋分以后的成绩X服从正态分布X~N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2:
,σ2近似为样本方差s2:
(i)利用正态分布,求P(50.41<X<79.59);
(ii)某市有20000名高三学生,记Y表示这20000名高三学生中赋分后该学科等级为A等(即得分大于79.59)的学生数,利用(i)的结果,求EY.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com