
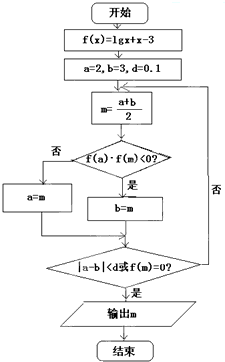
 如图是用二分法求方程lg x=3-x的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为
如图是用二分法求方程lg x=3-x的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为 | 根所在区间 | 区间端点函数值符号 | 中点值 | 中点函数值符号 |
| (2,3) | f(2)<0,f(3)>0 | 2.5 | f(2.5)<0 |
| (2.5,3) | f(2.5)<0,f(3)>0 | 2.75 | f(2.75)>0 |
| (2.5,2.75) | f(2.5)<0,f(2.75)>0 | 2.625 | f(2.625)>0 |
| (2.5,2.625) | f(2.5)<0,f(2.625)>0 | 2.5625 | f(2.5625)<0 |
| (2.5625,2.625) | f(2.5625)<0,f(2.625)>0 | 2.59375 | f(2.59375)>0 |
| (2.5625,2.59375) | f(2.5625)<0,f(2.59375)>0 | 2.578125 | f(2.578125)<0 |
| (2.578125,2.59375) | f(2.578125)<0,f(2.59375)>0 |


科目:高中数学 来源: 题型:
 (2011•沈阳二模)已知图象不间断的函数f(x)是区间[a,b]上的单调函数,且在区间(a,b)上存在零点.如图是用二分法求方程f(x)=0近似解的程序框图,判断框内可以填写的内容有如下四个选择:
(2011•沈阳二模)已知图象不间断的函数f(x)是区间[a,b]上的单调函数,且在区间(a,b)上存在零点.如图是用二分法求方程f(x)=0近似解的程序框图,判断框内可以填写的内容有如下四个选择:查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•深圳二模)如图是用二分法求方程x2-2=0近似解的程序框图,若输入x1=1,x2=2,?=0.3,则输出的m是
(2013•深圳二模)如图是用二分法求方程x2-2=0近似解的程序框图,若输入x1=1,x2=2,?=0.3,则输出的m是查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
 如图是用二分法求方程lg x=3-x的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为 如图是用二分法求方程lg x=3-x的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为
|
查看答案和解析>>
科目:高中数学 来源: 题型:
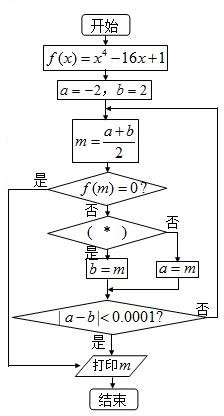 (2013•韶关三模)如图是用二分法求方程x4-16x+1=0在[-2,2]的近似解的程序框图,要求解的精确度为0.0001,则(*)处应填的内容是
(2013•韶关三模)如图是用二分法求方程x4-16x+1=0在[-2,2]的近似解的程序框图,要求解的精确度为0.0001,则(*)处应填的内容是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com