
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 8 | x | 3 | 2 |
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 27 | 18 |
| 生产能力分组 工人类别 | [110,130) | [130,150) | 总计 |
| A类工人 | 20 | 5 | 25 |
| B类工人 | 30 | 45 | 75 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据总体数和样本容量,得到每个个体被抽到的概率,得到两个组各自需要抽取的人数,减去已知的人数,得到x,y的值,根据所给的两个频率分布表做出频率分布直方图.
(2)先根据所给的数据得到列联表,把列联表中的数据代入求观测值的公式,求出这组数据的观测值,把观测值同临界值表中的数据进行比较得到对应的概率的值,得到在犯错误的概率不超过0.001的前提下,认为工人的生产能力与工人的类别有关系;
(3)求出X的取值,得出相应的概率,即可得出期望.
解答 解:(1)∵从该工厂的工人中抽取100名工人,且该工厂中有250名A类工人750名B类工人,
∴要从A类工人中抽取25名,从B类工人中抽取75名,(2分)
∴x=25-8-3-2=12,y=75-6-27-18=24.(4分)
| 生产能力分组 工人类别 | [110,130) | [130,150) | 总计 |
| A类工人 | 20 | 5 | 25 |
| B类工人 | 30 | 45 | 75 |
| 总计 | 50 | 50 | 100 |
| X | 0 | 1 | 2 |
| P(X) | 0.3 | 0.6 | 0.1 |
点评 本题考查频率分布直方图,考查独立性检验的应用,考查分层抽样,考查分布列与期望,本题解题的关键是根据根据分层抽样做出两个数值,再进行下面的画图和列表,本题是一个中档题目.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.
已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4-2ln2,+∞) | B. | [1+$\sqrt{e}$,+∞) | C. | [4-2ln2,1+$\sqrt{e}$) | D. | (-∞,1+$\sqrt{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
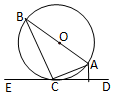 如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com