Question

【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分，并将其得分作为该选手的成绩，成绩大于等于分的选手定为合格选手，直接参加第二轮比赛，大于等于分的选手将直接参加竞赛选拔赛.已知成绩合格的名参赛选手成绩的频率分布直方图如图所示，其中的频率构成等比数列.

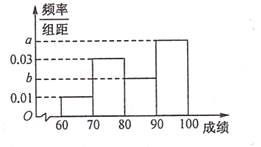
（1）求的值；

（2）估计这名参赛选手的平均成绩；

（3）根据已有的经验，参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为，假设每名选手能否通过竞赛选拔赛相互独立，现有名选手进入竞赛选拔赛，记这名选手在竞赛选拔赛中通过的人数为随机变量，求的分布列和数学期望.

Answer 1

【答案】(1) ；(2)84；(3)分布列见解析，1.

【解析】

(1)利用频率分布直方图的性质列式求解即可.

(2) 利用频率分布直方图求平均数的方法求解即可.

(3)易得随机变量满足二项分布,再根据二项分布的分布列与数学期望求解即可.

解:(1)由题意,得

解得

(2)估计这名选手的平均成绩为.

(3)由题意知,,

则可能取值为,

所以

所以的分布列为

故的数学期望为.