练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】[选修4－4：坐标系与参数方程]

    在平面直角坐标系中，直线的参数方程为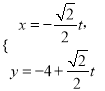（其中t为参数），现以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为．

    （1）写出直线l普通方程和曲线C的直角坐标方程；

    （2）过点且与直线平行的直线交于， 两点，求.

    【答案】(1)见解析;(2) .

    【解析】试题分析：（1）先根据加减消元得直线l的普通方程，再根据将曲线C的极坐标方程化为直角坐标方程；（2）先求直线参数方程标准形式，再代入曲线C的直角坐标方程，根据参数几何意义得，最后利用韦达定理代入求值.

    试题解析：（1）由消去参数t，得直线l的普通方程为．

    又由得，

    所以曲线的直角坐标方程为．

    （2） 过点且与直线平行的直线的参数方程为

    将其代入得，

    则，

    所以．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某商品促销活动设计了一个摸奖游戏：在一个口袋中装有4个红球和6个白球，这些球除颜色外完全相同，顾客一次从中摸出3个球，若3个都是白球则无奖励，若有1个红球则奖励10元购物券，若有2个红球则奖励20元购物券，若3个都是红球则奖励30元购物券.

    （Ⅰ）求中奖的概率；

    （Ⅱ）求顾客摸奖一次获得购物券奖励的平均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（原创题）已知点是椭圆和抛物线 的公共焦点， 是椭圆的长轴的两个端点，点是与 在第二象限的交点，且.

    (I) 求椭圆 的方程；

    (II) 点为直线上的动点，过点作抛物线的两条切线，切点分别为.直线交椭圆 于两点，设△的面积为，△的面积为，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图，则下列结论中不一定正确的是（ ）

    A. 互联网行业从业人员中90后占一半以上

    B. 互联网行业中从事技术岗位的人数超过总人数的

    C. 互联网行业中从事运营岗位的人数90后比80前多

    D. 互联网行业中从事运营岗位的人数90后比80后多

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在四棱锥P－ABCD中，底面ABCD是矩形，且AD＝2，AB＝1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．

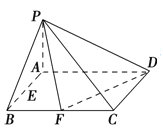
    (1)证明：PF⊥FD；

    (2)判断并说明PA上是否存在点G，使得EG∥平面PFD；

    (3)若PB与平面ABCD所成的角为45°，求二面角A－PD－F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某田径队有三名短跑运动员，根据平时训练情况统计甲、乙、丙三人100米跑（互不影响）的成绩合格的概率分别为，，，若对这三名短跑运动员的100米跑的成绩进行一次检测.

    （1）求三人都合格的概率；

    （2）求三人都不合格的概率；

    （3）求出现几人合格的概率最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题p：实数x满足，命题：实数x满足

    (1)若，且为真，求实数的取值范围；

    (2)若，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校统计了本校高一年级学生期中考试的数学成绩，其数学成绩(满分150分)均在内，将这些成绩分成5组，得到如图所示的频率分布直方图.

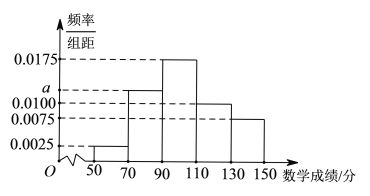
    （1）求a的值；

    （2）求该校高一年级学生期中考试的数学成绩的中位数(结果保留一位小数).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知球O是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）A-BCD的外接球，BC=3，，点E在线段BD上，且BD=3BE，过点E作圆O的截面，则所得截面圆面积的取值范围是__.

    查看答案和解析>>

    同步练习册答案