
【题目】已知函数g(x)=ex , f(x)= ![]() ,f(x)是定义在R上的奇函数.
,f(x)是定义在R上的奇函数.
(1)求a,b的值;
(2)若关于t的方程f(2t2﹣mt)+f(1﹣t2)=0有两个根α、β,且α>0,1<β<2,求实数m的取值范围.
【答案】
(1)解:f(x)是定义在R上的奇函数,
∴f(0)= ![]() ,即a=1.又f(﹣1)=﹣f(1),即
,即a=1.又f(﹣1)=﹣f(1),即 ![]() ,可得b=e.
,可得b=e.
所以f(x)= ![]() .
.
又f(﹣x)= ![]() ,
,
所以a=1,b=e成立
(2)解:f(x)= ![]() ,易得f(x)在R上单调递减.
,易得f(x)在R上单调递减.
方程f(2t2﹣mt)+f(1﹣t2)=0可转化为f(2t2﹣mt)=﹣f(1﹣t2),又函数f(x)是奇函数,则
f(2t2﹣mt)=f(t2﹣1).又函数f(x)在R上单调递减,
所以2t2﹣mt=t2﹣1,即t2﹣mt+1=0.
考虑函数h(t)=t2﹣mt+1,
(i)若α=1或2,则m=2或 ![]() ,易得
,易得 ![]() ,与β∈(1,2)矛盾;
,与β∈(1,2)矛盾;
(ii)若0<α<1或α>2,则h(1)h(2)<0,即(2﹣m)(5﹣2m)<0, ![]() ;
;
(iii)若1<α<2,则只需满足 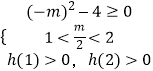 ,
,
由以上(i)、(ii)、(iii)可知 ![]()
【解析】(1)根据奇函数的定义求解;(2)利用奇函数的性质转化为一元二次不等式,借助与一元二次函数的关系进行判断.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知长方体ABCD﹣A'B'C'D'中,AB=4,AD=3,AA'=2; 
(1)求出异面直线AC'和BD所成角的余弦值;
(2)找出AC'与平面D'DBB'的交点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点.
(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 满足f(0)=0.
满足f(0)=0.
(1)求a,f(﹣2)的值,判断函数f(x)的奇偶性并说明理由;
(2)判断该函数在R上的单调性(不要求证明),解不等式f(x2+x)< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点相同,
的焦点相同,![]() ,
,![]() 为椭圆的左、右焦点.
为椭圆的左、右焦点.![]() 为椭圆上任意一点,△
为椭圆上任意一点,△![]() 面积的最大值为1.
面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() :
:![]()
![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
(i)若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(ii)若直线![]() 的斜率时直线
的斜率时直线![]() ,
,![]() 斜率的等比中项,求△
斜率的等比中项,求△![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线l1:y=x,l2:y=x+2与圆C:x2+y2﹣2mx﹣2ny=0的四个交点把圆C分成的四条弧长相等,则m=( )
A.0或1
B.0或﹣1
C.1或﹣1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com