
 ,
, 分别是与x轴,y轴正方向同向的单位向量,若向量
分别是与x轴,y轴正方向同向的单位向量,若向量 =x
=x +y
+y ,则把有序数对(x,y)叫做向量
,则把有序数对(x,y)叫做向量 在坐标系xOy中的坐标.设
在坐标系xOy中的坐标.设 ,
, ,给出下列三个命题:
,给出下列三个命题: =(1,0);
=(1,0);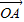 ⊥
⊥ ;
;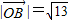 .
.
 •
•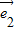 ═
═ 且
且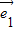 2=
2=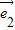 2=1,从而得到
2=1,从而得到 •
• =(-
=(-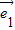 +2
+2 )•
)• =0,得
=0,得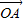 ⊥
⊥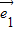 ,得②正确;同理算出
,得②正确;同理算出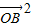 =(3
=(3 +2
+2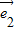 )2=19,得到
)2=19,得到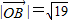 ,故③不正确.由此可得本题答案.
,故③不正确.由此可得本题答案.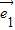 =x
=x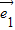 +y
+y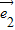 ,当且仅当x=1、y=0
,当且仅当x=1、y=0 的坐标为(1,0),即
的坐标为(1,0),即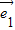 =(1,0),故①正确;
=(1,0),故①正确;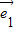 •
• =|
=|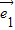 |•|
|•|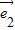 |cos60°=
|cos60°= ,
, 2=
2=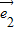 2=1
2=1 •
• =(-
=(- +2
+2 )•
)• =-
=-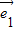 2+2
2+2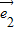 •
• =-1+2×
=-1+2× =0
=0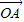 ⊥
⊥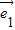 ,得②正确;
,得②正确;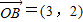 =3
=3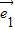 +2
+2
 =(3
=(3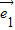 +2
+2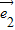 )2=9
)2=9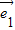 2+12
2+12 •
• +4
+4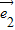 2=9+6+4=19
2=9+6+4=19 ,故③不正确
,故③不正确

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
 如图,设Ox,Oy是平面内相交成60°角的两条数轴,
如图,设Ox,Oy是平面内相交成60°角的两条数轴,| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
| OA |
| OB |
| e1 |
| OA |
| e1 |
| OB |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
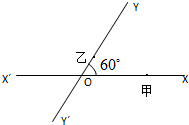 如图,有两条相交成60°的直路XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后甲沿XX′方向用2km/h的速度,乙沿Y′Y方向用4km/h的速度同时步行.设t小时后甲在XX′上点A处,乙在YY′上点B处.
如图,有两条相交成60°的直路XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后甲沿XX′方向用2km/h的速度,乙沿Y′Y方向用4km/h的速度同时步行.设t小时后甲在XX′上点A处,乙在YY′上点B处.查看答案和解析>>
科目:高中数学 来源: 题型:044
如图,设
Ox、Oy是平面内相交成60°角的两条数轴, 、
、 分别是与x轴、y轴正方向同向的单位向量,若向量
分别是与x轴、y轴正方向同向的单位向量,若向量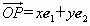 ,则把有序数对(x,y)叫做向量
,则把有序数对(x,y)叫做向量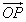 在坐标系xOy中的坐标.假设
在坐标系xOy中的坐标.假设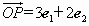 ,
,
(1)
计算 的大小;
的大小;
(2)
由平面向量基本定理,本题中向量坐标的规定是否合理?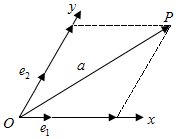
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,有两条相交成60°的直路XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后甲沿XX′方向用2km/h的速度,乙沿Y′Y方向用4km/h的速度同时步行.设t小时后甲在XX′上点A处,乙在YY′上点B处.
如图,有两条相交成60°的直路XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后甲沿XX′方向用2km/h的速度,乙沿Y′Y方向用4km/h的速度同时步行.设t小时后甲在XX′上点A处,乙在YY′上点B处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com