
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x-b|的最小值为1.
(1)证明:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某单位共有500名职工,其中不到35岁的有125人,35-49岁的有a人,50岁及以上的有b人,现用分层抽样的方法,从中抽出100名职工了解他们的健康情况:
(1)求不到35岁的职工要抽取的人数;
(2)如果已知35-49岁的职工抽取了56人,求a的值,并求50岁及以上的职工要抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用
的关系,可选用
A.一次函数B.二次函数
C.指数型函数D.对数型函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=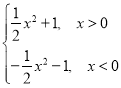
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2BC,P是线段AB中点,![]() 平面ABCD.
平面ABCD.
(1)求证:![]() 平面EPC;
平面EPC;
(2)问在EP上是否存在点F,使平面![]() 平面BFC?若存在,求出
平面BFC?若存在,求出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
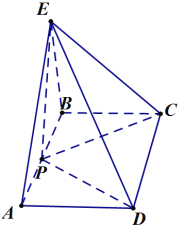
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,三棱锥![]() 的体积是18,求
的体积是18,求![]() 点到平面
点到平面![]() 的距离.
的距离.
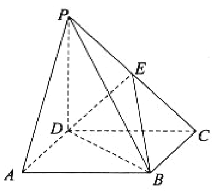
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的椭圆
的椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() 、
、![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() ,
, ![]() ,
, ![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 、
、![]() 、
、![]() 、
、![]() 四位贵宾,应分别对应坐在
四位贵宾,应分别对应坐在![]() 、
、![]() 、
、![]() 、
、![]() 四个席位上,现在这四人均未留意,在四个席位上随便就座.
四个席位上,现在这四人均未留意,在四个席位上随便就座.
(1)求这四人恰好都坐在自己席位上的概率;
(2)求这四人恰好都没坐在自己席位上的概率;
(3)求这四人恰好有![]() 位坐在自己席位上的概率.
位坐在自己席位上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com