
(本小题12分)
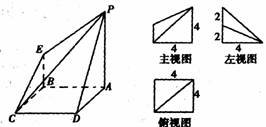
下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]()
![]() 面
面![]() ;
;
(Ⅱ)证明![]() 面
面![]() ;
;
(Ⅲ)求面![]() 与面
与面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
 |
答案
解: (Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,
 ∴PD⊥AF,
∴PD⊥AF,
又∵CD⊥DA,CD⊥PA,PA∩DA=A,
∴CD⊥面ADP,
∴CD⊥AF.又CD∩DP=D, ∴AF⊥面PCD. ------------- 4分
(Ⅱ)取PC的中点M,AC与BD的交点为N,连结MN,
∴MN=![]() PA,MN∥PA,
PA,MN∥PA,
∴MN=EB,MN∥EB,故四边形BEMN为平行四边形,
∴EM∥BN,又EM![]() 面PEC,∴BD∥面PEC. -------------7分
面PEC,∴BD∥面PEC. -------------7分
(Ⅲ)分别以BC,BA,BE为x,y,z轴建立空间直角坐标系,
则C( 4,0,0),D(4 ,4 , 0),E(0,0,2),A(0,4 ,0),P(0,4,4),
∵F为PD的中点,∴F(2,4,2).
∵AF⊥面PCD,∴![]() 为面PCD的一个法向量,
为面PCD的一个法向量,
![]() =(-2,0,-2),设平面PEC的法向量为
=(-2,0,-2),设平面PEC的法向量为![]() =(x,y ,z),
=(x,y ,z),
则 ,
,
∴![]() ,令x=1,∴
,令x=1,∴![]() , -------------10分
, -------------10分
∴
∴![]() 与
与![]() 的夹角为
的夹角为![]() .
.
面PEC与面PDC所成的二面角(锐角)的余弦值为![]() . -------------12分
. -------------12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年辽宁省沈阳市高三高考领航考试(一)理科数学试卷(解析版) 题型:解答题
(本小题12分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
|
x |
6 |
8 |
10 |
12 |
|
y |
2 |
3 |
5 |
6 |
(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: )
)
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-3 3.2回归分析练习卷(解析版) 题型:解答题
(本小题12分) 适当饮用葡萄酒可以预防心脏病,下表中的信息是19个发达国家一年中平均每人喝葡萄酒摄取酒精的升数z以及一年中每10万人因心脏病死亡的人数,
|
国家 |
澳大利亚 |
奥地利 |
比利时 |
加拿大 |
丹麦 |
芬兰 |
法国 |
冰岛 |
爰尔兰 |
意大利 |
|
x |
2.5 |
3.9 |
2.9 |
2.4 |
2.9 |
0.8 |
9.1 |
0.8 |
0.7 |
7.9 |
|
y |
211 |
167 |
131 |
191 |
220 |
297 |
71 |
221 |
300 |
107 |
|
国家 |
荷兰 |
新西兰 |
挪威 |
西班牙 |
瑞典 |
瑞士 |
英国 |
美国 |
德国 |
|
x |
1.8 |
1.9 |
0.8 |
6.5 |
1.6 |
5.8 |
1.3 |
1.2 |
2.7 |
|
y |
167 |
266 |
227 |
86 |
207 |
115 |
285 |
199 |
172 |
(1)画出散点图,说明相关关系的方向、形式及强度;
(2)求出每10万人中心脏病死亡人数,与平均每人从葡萄酒得到的酒精x(L)之间的线性回归方程.
(3)用(2)中求出的方程来预测以下两个国家的心脏病死亡率,其中一个国家的成人每年平均从葡萄酒中摄取1L的酒精,另一国则是8 L.
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期期中考试文科数学试题(解析版) 题型:解答题
(本小题12分)下表提供了工厂技术改造后某种型号设备的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)的几组对照数据:
(万元)的几组对照数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)若知道 对
对 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
查看答案和解析>>
科目:高中数学 来源:2014届甘肃省高一下学期第一次阶段考试数学试卷(解析版) 题型:解答题
(本小题12分)
从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
|
甲 |
7 |
8 |
6 |
8 |
6 |
5 |
9 |
10 |
7 |
4 |
|
乙 |
9 |
5 |
7 |
8 |
7 |
6 |
8 |
6 |
7 |
7 |
(1) 计算甲乙两人射击命中环数的平均数和方差;
(2) 比较两人的成绩,然后决定选择哪一人参赛.
查看答案和解析>>
科目:高中数学 来源:2014届四川省攀枝花市高一上学期期中考试数学试卷 题型:解答题
(本小题12分)已知函数 是定义在
是定义在 的函数,对任意实数
的函数,对任意实数 ,
,
都有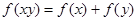 ,且当
,且当 时,
时, ;
; .
.
(1)求 ; (2)在我们所学的函数中写出一个符合条件的函数;
; (2)在我们所学的函数中写出一个符合条件的函数;
(3)在条件(2)下解不等式: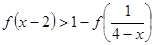 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com