
【题目】已知函数![]() (
(![]() 为常数),曲线
为常数),曲线![]() 在与
在与![]() 轴的交点A处的切线与
轴的交点A处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)若存在不相等的实数![]() 使
使![]() 成立,试比较
成立,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)a=2,在区间(-∞,ln 2)上单调递减,在(ln 2,+∞)上单调递增.(2)x1+x2<2ln 2
【解析】
(1)由导数的几何意义得到![]() ,求出a的值,再求函数
,求出a的值,再求函数![]() 的单调区间.(2) 令g(x)=
的单调区间.(2) 令g(x)=![]() (x)-
(x)-![]() (2ln 2-x)=ex-
(2ln 2-x)=ex-![]() -4x+4ln 2(x≥ln 2),
-4x+4ln 2(x≥ln 2),
利用导数得到函数g(x) 在(ln 2,+∞)上单调递增,即![]() (x)>
(x)>![]() (2ln 2-x),不妨设x1<ln 2<x2,所以
(2ln 2-x),不妨设x1<ln 2<x2,所以![]() (x2)>
(x2)>![]() (2ln 2-x2),再证明x1+x2<2ln 2.
(2ln 2-x2),再证明x1+x2<2ln 2.
(1)由![]() ,
,
得![]() .且f(x)与y轴交于A(0.0)
.且f(x)与y轴交于A(0.0)
所以![]() ,所以a=2,
,所以a=2,
所以![]() ,
,![]() .
.
由![]() >0,得x>ln 2.
>0,得x>ln 2.
所以函数![]() 在区间(-∞,ln 2)上单调递减,在(ln 2,+∞)上单调递增.
在区间(-∞,ln 2)上单调递减,在(ln 2,+∞)上单调递增.
(2)证明:设x>ln 2,所以2ln 2-x<ln 2,
![]() (2ln 2-x)=e(2ln 2-x)-2(2ln 2-x)-1
(2ln 2-x)=e(2ln 2-x)-2(2ln 2-x)-1
=![]() +2x-4ln 2-1.
+2x-4ln 2-1.
令g(x)=![]() (x)-
(x)-![]() (2ln 2-x)=ex-
(2ln 2-x)=ex-![]() -4x+4ln 2(x≥ln 2),
-4x+4ln 2(x≥ln 2),
所以g′(x)=ex+4e-x-4≥0,
当且仅当x=ln 2时,等号成立,
所以g(x)=![]() (x)-
(x)-![]() (2ln 2-x)在(ln 2,+∞)上单调递增.
(2ln 2-x)在(ln 2,+∞)上单调递增.
又g(ln 2)=0,所以当x>ln 2时,g(x)=![]() (x)-
(x)-![]() (2ln 2-x)>g(ln 2)=0,
(2ln 2-x)>g(ln 2)=0,
即![]() (x)>
(x)>![]() (2ln 2-x),不妨设x1<ln 2<x2,所以
(2ln 2-x),不妨设x1<ln 2<x2,所以![]() (x2)>
(x2)>![]() (2ln 2-x2),
(2ln 2-x2),
又因为![]() (x1)=
(x1)=![]() (x2),所以
(x2),所以![]() (x1)>
(x1)>![]() (2ln 2-x2),
(2ln 2-x2),
由于x2>ln 2,所以2ln 2-x2<ln 2,
因为x1<ln 2,由(1)知函数y=![]() (x)在区间(-∞,ln 2)上单调递减,
(x)在区间(-∞,ln 2)上单调递减,
所以x1<2ln 2-x2,
即x1+x2<2ln 2.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
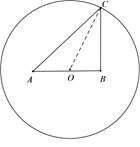
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,![]() 两点为喷泉,圆心
两点为喷泉,圆心![]() 为
为![]() 的中点,其中
的中点,其中![]() 米,半径
米,半径![]() 米,市民可位于水池边缘任意一点
米,市民可位于水池边缘任意一点![]() 处观赏.
处观赏.
(1)若当![]() 时,
时,![]() ,求此时
,求此时![]() 的值;
的值;
(2)设![]() ,且
,且![]() .
.
(i)试将![]() 表示为
表示为![]() 的函数,并求出
的函数,并求出![]() 的取值范围;
的取值范围;
(ii)若同时要求市民在水池边缘任意一点![]() 处观赏喷泉时,观赏角度
处观赏喷泉时,观赏角度![]() 的最大值不小于
的最大值不小于![]() ,试求
,试求![]() 两处喷泉间距离的最小值.
两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为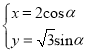 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换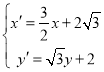 得到曲线
得到曲线![]() ,以原点为极点、
,以原点为极点、![]() 轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]()
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数,
为参数, ![]() ),将曲线
),将曲线![]() 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线![]() .
.
(1)以原点为极点, ![]() 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() (
(![]() 为参数)与
为参数)与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取,他们分别被哪个学校录取,同学们做了如下的猜想
甲同学猜:曾玉被武汉大学录取,李梦被复旦大学录取
同学乙猜:刘云被清华大学录取,张熙被北京大学录取
同学丙猜:曾玉被复旦大学录取,李梦被清华大学录取
同学丁猜:刘云被清华大学录取,张熙被武汉大学录取
结果,恰好有三位同学的猜想各对了一半,还有一位同学的猜想都不对
那么曾玉、刘云、李梦、张熙四人被录取的大小可能是( )
A.北京大学、清华大学、复旦大学、武汉大学
B.武汉大学、清华大学、复旦大学、北京大学
C.清华大学、北京大学、武汉大学 、复旦大学
D.武汉大学、复旦大学、清华大学、北京大学
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com