
【题目】某校为了解该校学生“停课不停学”的网络学习效率,随机抽查了高一年级100位学生的某次数学成绩,得到如图所示的频率分布直方图:
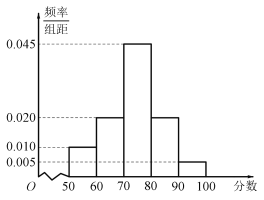
(1)估计这100位学生的数学成绩的平均值![]() .(同一组中的数据用该组区间的中点值代表);
.(同一组中的数据用该组区间的中点值代表);
(2)根据整个年级的数学成绩,可以认为学生的数学成绩![]() 近似地服从正态分布
近似地服从正态分布![]() 经计算,(1)问中样本标准差
经计算,(1)问中样本标准差![]() 的近似值为10.用样本平均数
的近似值为10.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
参考数据:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]()
(3)该年级1班的数学老师为了能每天督促学生的网络学习,提高学生每天的作业质量及学习数学的积极性,特意在微信上设计了一个每日作业小程序,每当学生提交的作业获得优秀时,就有机会参与一次小程序中“玩游戏,得奖励积分”的活动,开学后可根据获得积分的多少领取老师相应的小奖品.小程序页面上有一列方格,共15格,刚开始有只小兔子在第1格,每点一下游戏的开始按钮,小兔子就沿着方格跳一下,每次跳1格或跳2格,概率均为![]() ,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第
,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求
是等比数列,并求![]() 的值.(获胜的概率)
的值.(获胜的概率)
【答案】(1)74(2)0.8186(3)见解析,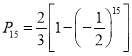
【解析】
(1)根据频率分布直方图直接结算即可;
(2)由![]() 可知
可知![]() ,根据参考数据,即可得出
,根据参考数据,即可得出![]() 的概率;
的概率;
(3)根据分类加法计数原理可知![]() ,构造等比数列可得
,构造等比数列可得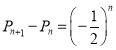 ,
,
利用累加法求出![]() ,即可求解.
,即可求解.
(1)![]()
(2)由![]() ,所以
,所以![]() ,
,
![]()
![]()
![]() .
.
(3)小兔子开始在第1格,为必然事件,![]() ,
,
点一下开始按钮,小兔子跳1格即移到第2格的概率为![]() ,即
,即![]() ,
,
小兔子移到第![]() 格的情况是下列两种,而且也只有两种情况.
格的情况是下列两种,而且也只有两种情况.
①小兔子先跳到第![]() 格,又点一下开始按钮跳了2格,其概率为
格,又点一下开始按钮跳了2格,其概率为![]() ;
;
②小兔了先跳到第![]() 格,乂点一下开始按钮跳了1格,其概率为
格,乂点一下开始按钮跳了1格,其概率为![]() ;
;
因为![]() ,所以
,所以![]() .
.
所以当![]() 时,
时,
数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,
所以![]() ,
,
![]()
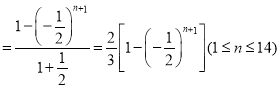 .
.
所以获胜的概率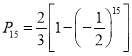 .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C关于x轴、y轴都对称,并且经过两点![]() ,
,
(1)求椭圆C的离心率和焦点坐标;
(2)D是椭圆C上到点A最远的点,椭圆C在点B处的切线l与y轴交于点E,求△BDE外接圆的圆心坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年3月10日湖北武汉某方舱医院“关门大吉”,某省驰援湖北“抗疫”的9名身高各不相同的医护人员站成一排合影留念,庆祝圆满完成“抗疫”任务,若恰好从中间往两边看都依次变低,则身高排第4的医护人员和最高的医护人员相邻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线G上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线G的方程.
(2)是否存在过F的直线l,使得l与曲线G相交于A,B两点,点A关于x轴的对称点为A',且△A'BF的面积等于4?若存在,求出此时直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(2)动直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,其中
,其中![]() 为坐标原点,证明
为坐标原点,证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上贏得一片赞誉.我国某口罩生产厂商在加大生产的同时.狠抓质量管理,不定时抽查口罩质量,该厂质检人员从某日所生产的口罩中随机抽取了100个,将其质量指标值分成以下五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
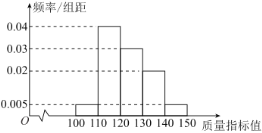
(1)规定:口罩的质量指标值越高,说明该口罩质量越好,其中质量指标值低于130的为二级口罩,质量指标值不低于130的为一级口罩.现从样本口罩中利用分层抽样的方法随机抽取8个口罩,再从中抽取3个,记其中一级口罩个数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在2020年“五一”劳动节前,甲,乙两人计划同时在该型号口罩的某网络购物平台上分别参加![]() 、
、![]() 两店各一个订单“秒杀”抢购,其中每个订单由
两店各一个订单“秒杀”抢购,其中每个订单由![]() 个该型号口罩构成.假定甲、乙两人在
个该型号口罩构成.假定甲、乙两人在![]() 、
、![]() 两店订单“秒杀”成功的概率分别为
两店订单“秒杀”成功的概率分别为![]() ,
,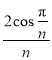 ,记甲、乙两人抢购成功的订单总数量、口罩总数量分别为
,记甲、乙两人抢购成功的订单总数量、口罩总数量分别为![]() ,
,![]() ,
,
①求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②求当![]() 的数学期望
的数学期望![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com