
【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( ) 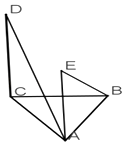
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值
【答案】D
【解析】解:取AC的中点O,连接OB,OE,则OB⊥AC,
∵DC⊥平面ABC,∴DC⊥OB,
∵DC∩AC=C,
∴OB⊥平面ADC,
∴OB⊥AD,
∵BE⊥AD,OB∩BE=B,
∴AD⊥平面BOE,
∴AD⊥OE,
∴∠AEO=∠CAD,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() ,
,
∴AE+CD=CD+ ![]() ≥2
≥2 ![]() ,当且仅当CD=
,当且仅当CD= ![]() 时,AE+DC有最小值,
时,AE+DC有最小值,
故选D.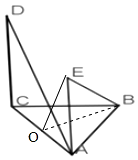
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
某电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(I)用![]() ,
,![]() 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用简单随机抽样方法从含有6个个体的总体中,抽取一个容量为2的样本,某一个体a“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到”的概率分别是
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四个命题的表述: ①直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,3);
②线段AB的端点B的坐标是(3,4),A在圆x2+y2=4上运动,则线段AB的中点M的轨迹方程 ![]() +(y﹣2)2=1
+(y﹣2)2=1
③已知M={(x,y)|y= ![]() },N={(x,y)|y=x+b},若M∩N≠,则b∈[﹣
},N={(x,y)|y=x+b},若M∩N≠,则b∈[﹣ ![]() ,
, ![]() ];
];
④已知圆C:(x﹣b)2+(y﹣c)2=a2(a>0,b>0,c>0)与x轴相交,与y轴相离,则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.
其中表述正确的是( (填上所有正确结论对应的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=0,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+log3n=log3bn , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,{bn}是等差数列,且a1=b1=1,a1+a2=b4 , b1+b2=a2 .
(1)求{an}与{bn}的通项公式;
(2)记数列{an+bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com