
【题目】![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),
=(sinx,sinx), ![]() =(﹣1,0)
=(﹣1,0)![]()
(1)若x= ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)若x∈[﹣ ![]() ,
, ![]() ],f(x)=λ
],f(x)=λ ![]()
![]() 的最大值为
的最大值为 ![]() ,求λ.
,求λ.
【答案】
(1)
解:当x= ![]() 时,
时, ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(﹣1,0),
=(﹣1,0),
∴ ![]() 与
与 ![]() 的夹角θ满足cosθ=
的夹角θ满足cosθ= ![]() =-
=- ![]() ,
,
∴ ![]() 与
与 ![]() 的夹角θ=
的夹角θ= ![]() ;
;
(2)
解:f(x)=λ ![]()
![]() =λ(sin2x+sinxcosx)
=λ(sin2x+sinxcosx)
=λ( ![]() +
+ ![]() sin2x)=
sin2x)= ![]() λsin(2x﹣
λsin(2x﹣ ![]() )+
)+ ![]() λ,
λ,
∵x∈[﹣ ![]() ,
, ![]() ],∴2x﹣
],∴2x﹣ ![]() ∈[﹣π,
∈[﹣π, ![]() ],
],
∴sin(2x﹣ ![]() )∈[﹣1,
)∈[﹣1, ![]() ],
],
当λ>0时,可得 ![]() λ /span>
λ /span>![]() +
+ ![]() λ=
λ= ![]() ,解得λ=
,解得λ= ![]() ;
;
当λ<0时,可得 ![]() λ(﹣1)+
λ(﹣1)+ ![]() λ=
λ= ![]() ,解得λ=﹣
,解得λ=﹣ ![]() ﹣1
﹣1
【解析】(1)当x= ![]() 时可得
时可得 ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(﹣1,0),由夹角公式可得;(2)可得f(x)=λ
=(﹣1,0),由夹角公式可得;(2)可得f(x)=λ ![]()
![]() =
= ![]() λsin(2x﹣
λsin(2x﹣ ![]() )+
)+ ![]() λ,由x的范围易得sin(2x﹣
λ,由x的范围易得sin(2x﹣ ![]() )∈[﹣1,
)∈[﹣1, ![]() ],分类讨论可得.
],分类讨论可得.
【考点精析】认真审题,首先需要了解数量积表示两个向量的夹角(设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则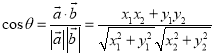 ),还要掌握两角和与差的正弦公式(两角和与差的正弦公式:
),还要掌握两角和与差的正弦公式(两角和与差的正弦公式:![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,连结
,连结![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,设直线
,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试探索当
,试探索当![]() 变化时,是否存在一条定直线
变化时,是否存在一条定直线![]() ,使得点
,使得点![]() 恒在直线
恒在直线![]() 上?若存在,请求出直线
上?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)图像上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() 叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: (1.)函数y=x3﹣x2+1图像上两点A、B的横坐标分别为1,2,则φ(A,B)>
叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: (1.)函数y=x3﹣x2+1图像上两点A、B的横坐标分别为1,2,则φ(A,B)> ![]() ;
;
(2.)存在这样的函数,图像上任意两点之间的“弯曲度”为常数;
(3.)设点A、B是抛物线,y=x2+1上不同的两点,则φ(A,B)≤2;
(4.)设曲线y=ex上不同两点A(x1 , y1),B(x2 , y2),且x1﹣x2=1,若tφ(A,B)<1恒成立,则实数t的取值范围是(﹣∞,1);
以上正确命题的序号为(写出所有正确的)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C1的参数方程为: ![]() (α为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2的极坐标方程为:ρ=cosθ. (Ⅰ)求曲线C2的直角坐标方程;
(α为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2的极坐标方程为:ρ=cosθ. (Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)若P,Q分别是曲线C1和C2上的任意一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】射击测试有两种方案,方案1:先在甲靶射击一次,以后都在乙靶射击;方案2:始终在乙靶射击,某射手命中甲靶的概率为![]() ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为![]() ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量![]() 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果![]() 的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
(1)如果该射手选择方案1,求其测试结束后所得分![]() 的分布列和数学期望E
的分布列和数学期望E![]() ;
;
(2)该射手选择哪种方案通过测试的可能性大?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解学生对周末家庭作业量的态度,拟采用分层抽样的方法分别从高一、高二、高三的高中生中随机抽取一个容量为200的样本进行调查,已知从700名高一、高二学生中共抽取了140名学生,那么该校有高三学生名.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2sinx,﹣cosx)、B( ![]() cosx,2cosx),记f(x)=
cosx,2cosx),记f(x)= ![]()
![]() .
.
(1)若x0是函数y=f(x)﹣1的零点,求tanx0的值;
(2)求f(x)在区间[ ![]() ,
, ![]() ]上的最值及对应的x的值.
]上的最值及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位有50名职工,现要从中抽取 10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(Ⅰ)若第5组抽出的号码为22,写出所有被抽出职工的号码;
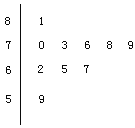
(Ⅱ)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的平均数、中位数和方差;
(Ⅲ)在(Ⅱ)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(![]() 73公斤)的职工,求体重为81公斤的职工被抽取到的概率.
73公斤)的职工,求体重为81公斤的职工被抽取到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com