解:(1)设等比数列{a
n}的公比为q,由a
5+a
7=8(a
2+a
4),
得
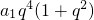
=8a
1q(1+q
2),
又∵a
1=2,q≠0,1+q
2>0,∴q=2,
数列{a
n}的通项公式为a
n=2
n,n∈N
*,
由题意有a
1b
1=(1-1)•2
1+1+2=2,∴b
1=1,
当n≥2时,a
nb
n=(n-1)•2
n+1-[(n-2)•2
n+2]=n•2
n,
∴b
n=n,.
故数列{b
n}的通项公式为b
n=n,n∈N
*.
(2)设数列{a
n}的第k项是数列{c
n}的第m
k项,即a
k=
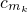
,k∈N
*,
当k≥2时,m
k=k+[1+2+…+(k-1)]=

,
m
62=
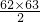
=1953,m
63=
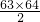
=2016,
设S
n表示数列{c
n}的前n项之和,
则S
2016=(a
1+a
2+…+a
63)+[(-1)
1•b
1+(-1)
2•2b
2+…+(-1)
62•62•b
62],
其中a
1+a
2+…+a
63=
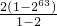
=2
64-2,
∵(-1)
n•nb
n=(-1)
n•n
2,
∴[(-1)
1•b
1+(-1)
2•2b
2+…+(-1)
62•62•b
62]=(-1)
1•1
2+(-1)
2•2
2+…+(-1)
62•62
2=(2
2-1
2)+(4
2-3
2)+…+(62
2-61
2)=(4×1-1)+(4×2-1)+(4×3-1)+…+(4×31-1)
=4×
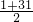
×31-31=1953,
∴S
2016=(2
64-2)+1953=2
64+1951,
从而S
2012=S
2016-(C
2013+C
2014+C
2015+C
2016)=2
64+1951-3(-1)
62×b
62-a
63=2
64+1951-3×62-2
63=2
63+1765.
所以数列{c
n}的前2012项之和为2
63+1765.
分析:(1)利用等比数列的通项公式,求出公比,从而求出数列{a
n}通项公式,再利用条件求数列{b
n}的通项公式;
(2)先判定数列{a
n}与数列{c
n}项数之间的关系,利用转化思想求和即可.
点评:本题考查了等比数列的通项公式,数列的通项与前n项和之间的关系,数列分组求和等知识,考查化归与转化的思想以及创新意识.

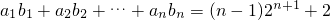 .
.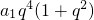 =8a1q(1+q2),
=8a1q(1+q2),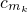 ,k∈N*,
,k∈N*, ,
,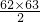 =1953,m63=
=1953,m63=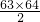 =2016,
=2016,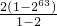 =264-2,
=264-2,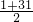 ×31-31=1953,
×31-31=1953,

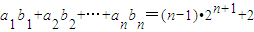 .
.