
【题目】若函数 ![]() 有两个极值点
有两个极值点![]() ,
,![]() ,其中
,其中 ![]() ,
,![]() ,且
,且![]() ,则方程
,则方程 ![]() 的实根个数为________________.
的实根个数为________________.
【答案】5
【解析】
由函数f(x)=﹣lnx+ax2+bx﹣a﹣2b有两个极值点x1,x2,可得2ax2+bx﹣1=0有两个不相等的正根,必有△=b2+8a>0.而方程2a(f(x))2+bf(x)﹣1=0的△1=△>0,可知此方程有两解且f(x)=x1或x2.再分别讨论利用平移变换即可解出方程f(x)=x1或f(x)=x2解的个数.
∵函数f(x)=﹣lnx+ax2+bx﹣a﹣2b有两个极值点x1,x2,
∴f′(x)=﹣![]() +2ax+b=
+2ax+b=![]() ,
,
即为2ax2+bx﹣1=0有两个不相等的正根,
∴△=b2+8a>0.解得x=![]() .
.
∵x1<x2,﹣![]() ,b>0,
,b>0,
∴x1=![]() ,x2=
,x2=![]() .
.
而方程2a(f(x))2+bf(x)﹣1=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2
即有0<x1<x2,:∵x1,x2>0又x1x2=﹣![]() >1
>1
∴x2>1,∵f(1)=﹣b<0∴f(x1)<0,
f(x2)>0.
①根据f′(x)画出f(x)的简图,
∵f(x2)=x2,由图象可知方程f(x)=x2有两解,方程f(x)=x1有三解.
综上①②可知:方程f(x)=x1或f(x)=x2共有5个实数解.
即关于x的方程2a(f(x))2+bf(x)﹣1=0的共有5不同实根.
故答案为:5


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(1)证明PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.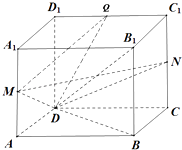
(1)求证:直线MN⊥平面B1BD;
(2)已知AA1=AB,AA1⊥AB,取线段C1D1的中点Q,求二面角Q﹣MD﹣N的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米。现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点F1(﹣c,0),F2(c,0)分别是椭圆C: ![]() =1(a>1)的左、右焦点,P为椭圆C上任意一点,且
=1(a>1)的左、右焦点,P为椭圆C上任意一点,且 ![]()
![]() 的最小值为0.
的最小值为0. 
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l,求四边形F1MNF2面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com