
【题目】(2016·贵阳第二次联考)在△ABC中,角A,B,C的对边分别为a,b,c,向量m=(a+b,sin A-sin C),向量n=(c,sin A-sin B),且m∥n.
(1)求角B的大小;
(2)设BC的中点为D,且AD=![]() ,求a+2c的最大值及此时△ABC的面积.
,求a+2c的最大值及此时△ABC的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:![]() 由条件利用两个向量共线的性质,正弦定理,余弦定理可得
由条件利用两个向量共线的性质,正弦定理,余弦定理可得![]() 的值,从而求得
的值,从而求得![]() 的值;
的值;
![]() 设
设![]() ,则在
,则在![]() 中,可知
中,可知![]() ,利用正弦定理求得
,利用正弦定理求得![]() 的值,可得
的值,可得![]() 的值,再利用正弦函数的定义域和值域求得
的值,再利用正弦函数的定义域和值域求得![]() 的最大值及此时
的最大值及此时![]() 的面积。
的面积。
解析:(1)因为m∥n,
所以(a+b)(sin A-sin B)-c(sin A-sin C)=0.
由正弦定理,得(a+b)(a-b)-c(a-c)=0,即a2+c2-b2=ac.
由余弦定理,得cosB=![]() =
=![]() =
=![]() .
.
因为B∈(0,π),所以B=![]() .
.
(2)设∠BAD=θ,则在△BAD中,
由B=![]() ,可知θ∈(0,
,可知θ∈(0,![]() ).
).
由正弦定理及AD=![]() ,得
,得![]() =
=![]() =
=![]() =2,
=2,
所以BD=2sin θ,AB=2sin(![]() -θ)=
-θ)=![]() cosθ+sin θ.
cosθ+sin θ.
所以a=2BD=4sin θ,c=AB=![]() cosθ+sin θ.
cosθ+sin θ.
从而a+2c=2![]() cos θ+6sin θ=4
cos θ+6sin θ=4![]() sin(θ+
sin(θ+![]() ).
).
由θ∈(0,![]() ),可知θ+
),可知θ+![]() ∈(
∈(![]() ,
,![]() ),
),
所以当θ+![]() =
=![]() ,即θ=
,即θ=![]() 时,a+2c取得最大值4
时,a+2c取得最大值4![]() .
.
此时a=2![]() ,c=
,c=![]() ,
,
所以S△ABC=![]() acsinB=
acsinB=![]() .
.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大豆,古称菽,原产中国,在中国已有五千年栽培历史。皖北多平原地带,黄河故道土地肥沃,适宜种植大豆。2018年春,为响应中国大豆参与世界贸易的竞争,某市农科院积极研究,加大优良品种的培育工作。其中一项基础工作就是研究昼夜温差大小与大豆发芽率之间的关系。为此科研人员分别记录了5天中每天100粒大豆的发芽数得如下数据表格:
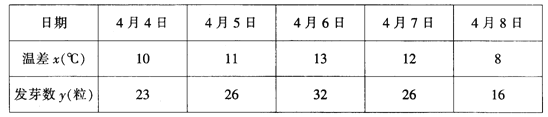
科研人员确定研究方案是:从5组数据中选3组数据求线性回归方程,再用求得的回归方程对剩下的2组数据进行检验.
(1)求剩下的2组数据恰是不相邻的2天数据的概率;
(2)若选取的是4月5日、6日、7日三天数据据此求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与实际数据的误差绝对值均不超过1粒,则认为得到的线性回归方程是可靠的,请检验(Ⅱ)中回归方程是否可靠?
注: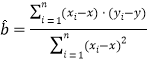
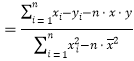 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边长分别为a,b,c,且满足a2+c2-b2=![]() ac.
ac.
(1)求角B的大小;
(2)若2bcos A=![]() (ccosA+acosC),BC边上的中线AM的长为
(ccosA+acosC),BC边上的中线AM的长为![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
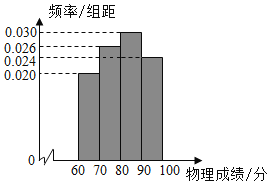
【题目】为了解某校高一1000名学生的物理成绩,随机抽查了部分学生的期中考试成绩,将数据整理后绘制成如图所示的频率分布直方图.
(1)估计该校高一学生物理成绩不低于80分的人数;
(2)若在本次考试中,规定物理成绩在m分以上(包括m分)的为优秀,该校学生物理成绩的优秀率大约为18%,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 直线AM,BM相交于点M,且它们的斜率之和为2.
直线AM,BM相交于点M,且它们的斜率之和为2.
(1)设![]() 且
且![]() ,求
,求![]() 的表达式,并写出函数
的表达式,并写出函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性?并给出证明;
的奇偶性?并给出证明;
(3)试用函数单调性的定义证明:![]() 在定义域上不是增函数,但在(0,1)∪(1,+
在定义域上不是增函数,但在(0,1)∪(1,+![]() )上为增函数.
)上为增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论:

①平面MENF⊥平面BDD′B′;
②直线AC∥平面MENF始终成立;
③四边形MENF周长L=f(x),x∈[0,1]是单调函数;
④四棱锥C′-MENF的体积V=h(x)为常数;
以上结论正确的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com