【题目】曲线y=1+ 
与直线kx﹣y﹣2k+5=0有两个交点时，实数k的取值范围是 ．
【答案】
【解析】解：化简曲线y=1+ 
，得x2+（y﹣1）2=4（y≥1） ∴曲线表示以C（0，1）为圆心，半径r=2的圆的上半圆．
∵直线kx﹣y﹣2k+5=0可化为y﹣5=k（x﹣2），
∴直线经过定点A（2，5）且斜率为k．
又∵半圆y=1+ 与直线kx﹣y﹣2k+5=0有两个相异的交点，
∴设直线与半圆的切线为AD，半圆的左端点为B（﹣2，1），
当直线的斜率k大于AD的斜率且小于或等于AB的斜率时，
直线与半圆有两个相异的交点．
由点到直线的距离公式，当直线与半圆相切时满足 
=2，
解之得k= 
，即kAD= ．
又∵直线AB的斜率kAB=1，∴直线的斜率k的范围为k∈ ．
故答案为 ．
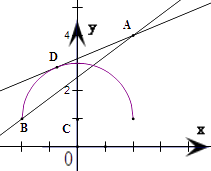
将曲线方程化简，可得曲线表示以C（0，1）为圆心、半径r=2的圆的上半圆．再将直线方程化为点斜式，可得直线经过定点A（2，5）且斜率为k．作出示意图，设直线与半圆的切线为AD，半圆的左端点为B（﹣2，1），当直线的斜率k大于AD的斜率且小于或等于AB的斜率时，直线与半圆有两个相异的交点．由此利用直线的斜率公式与点到直线的距离公式加以计算，可得实数k的取值范围．
一诺书业暑假作业快乐假期云南美术出版社系列答案科目：高中数学 来源： 题型：
【题目】已知 
=（sinx，cosx）， 
=（sinx，k）， 
=（﹣2cosx，sinx﹣k）．
（1）当x∈[0， 
]时，求| + |的取值范围；
（2）若g（x）=（ + ） ，求当k为何值时，g（x）的最小值为﹣ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C：（x﹣2）2+y2=9，直线l：x+y=0．
（1）求过圆C的圆心且与直线l垂直的直线n的方程；
（2）求与圆C相切，且与直线l平行的直线m的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C1：x2+y2=4与圆C2：（x﹣1）2+（y﹣3）2=4，过动点P（a，b）分别作圆C1、圆C2的切线PM，PN，（M，N分别为切点），若|PM|=|PN|，则a2+b2﹣6a﹣4b+13的最小值是（ ）
A.5
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题：①函数f（x）＝sin2x一cos2x的最小正周期是
；
②在等比数列〔
｝中，若
，则a3＝士2；
③设函数f（x）＝
，若
有意义，则
④平面四边形ABCD中， 
，则四边形ABCD是
菱形． 其中所有的真命题是：( )
A. ①②④ B. ①④ C. ③④ D. ①②③
查看答案和解析>>
科目：高中数学 来源： 题型：
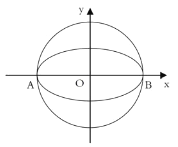
【题目】如图，椭圆
的离心率为
，其左顶点
在圆
上.
（1）求椭圆
的方程；
（2）直线
与椭圆的另一个交点为
，与圆
的另一个交点为
.
（ⅰ）当
时，求直线
的斜率；
（ⅱ）是否存在直线，使
？若存在，求出直线的斜率；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|ax﹣1|﹣（a﹣1）x
（1）当a= 
时，满足不等式f（x）＞1的x的取值范围为；若函数f（x）的图象与x轴没有交点，则实数a的取值范围为 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】圆C：（x﹣1）2+（y﹣2）2=25，直线l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）．
（1）证明：不论m取什么数，直线l与圆C恒交于两点；
（2）求直线l被圆C截得的线段的最短长度，并求此时m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
