
【题目】已知半径为 ![]() ,圆心在直线l1:x﹣y+1=0上的圆C与直线l2:
,圆心在直线l1:x﹣y+1=0上的圆C与直线l2: ![]() x﹣y+1﹣
x﹣y+1﹣ ![]() =0相交于M,N两点,且|MN|=
=0相交于M,N两点,且|MN|= ![]()
(1)求圆C的标准方程;
(2)当圆心C的横、纵坐标均为整数时,若对任意m∈R,直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,求实数a的取值范围.
+1=0与圆C恒有公共点,求实数a的取值范围.
【答案】
(1)解:由题意,设C(a,a+1),圆心到直线的距离d= 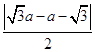 =
= ![]() ,
,
∴a=0或3+ ![]() ,
,
∴圆C的标准方程为x2+(y﹣1)2=5或(x﹣3﹣ ![]() )2+(y﹣4﹣
)2+(y﹣4﹣ ![]() )2=5;
)2=5;
(2)解:圆C的标准方程为x2+(y﹣1)2=5,对任意m∈R,
直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,
+1=0与圆C恒有公共点,
∴ 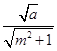 ≤
≤ ![]() ,
,
∴0≤a≤5(m2+1),∴0≤a≤5.
【解析】(1)由题意,设C(a,a+1),圆心到直线的距离d= ![]() =
= ![]() ,求出a,可得圆C的标准方程;(2)圆C的标准方程为x2+(y﹣1)2=5,对任意m∈R,直线l3:mx﹣y+
,求出a,可得圆C的标准方程;(2)圆C的标准方程为x2+(y﹣1)2=5,对任意m∈R,直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,
+1=0与圆C恒有公共点, ![]() ≤
≤ ![]() ,即可求实数a的取值范围.
,即可求实数a的取值范围.
【考点精析】掌握直线与圆的三种位置关系是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx+φ)+cos(ωx+φ) ![]() 的最小正周期为π,且f(﹣x)=f(x),则( )
的最小正周期为π,且f(﹣x)=f(x),则( )
A.f(x)在 ![]() 单调递减
单调递减
B.f(x)在( ![]() ,
, ![]() )单调递减
)单调递减
C.f(x)在(0, ![]() )单调递增
)单调递增
D.f(x)在( ![]() ,
, ![]() )单调递增
)单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6道题,其中3道甲类题,2道乙类题,张同学从中任取2道题解答.试求: (Ⅰ)所取的2道题都是甲类题的概率;
(Ⅱ)所取的2道题不是同一类题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.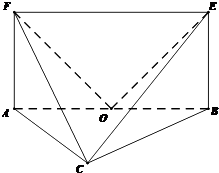
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足对于任意实数a,b,c,都有f(a),f(b),f(c)为某三角形的三边长,则成f(x)为“可构造三角形函数”,已知f(x)= ![]() 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A.[﹣1,0]
B.(﹣∞,0]
C.[﹣2,﹣1]
D.[﹣2,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需把函数y=sin2x的图象上所有的点( )
)的图象,只需把函数y=sin2x的图象上所有的点( )
A.向左平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A为椭圆 ![]() =1(a>b>0)上的一个动点,弦AB,AC分别过左右焦点F1 , F2 , 且当线段AF1的中点在y轴上时,cos∠F1AF2=
=1(a>b>0)上的一个动点,弦AB,AC分别过左右焦点F1 , F2 , 且当线段AF1的中点在y轴上时,cos∠F1AF2= ![]() . (Ⅰ)求该椭圆的离心率;
. (Ⅰ)求该椭圆的离心率;
(Ⅱ)设 ![]() ,试判断λ1+λ2是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
,试判断λ1+λ2是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析,得到如下数据:
记忆能力x | 4 | 6 | 8 | 10 |
识图能力y | 3 | ﹡﹡﹡ | 6 | 8 |
由于某些原因,识图能力的一个数据丢失,但已知识图能力样本平均值是5.5.
(Ⅰ)求丢失的数据;
(Ⅱ)经过分析,知道记忆能力x和识图能力y之间具有线性相关关系,请用最小二乘法求出y关于x的线性回归方程 ![]() ;
;
(III)若某一学生记忆能力值为12,请你预测他的识图能力值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com