练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=3sin（ωx+） 的部分图象如图所示，A，B两点之间的距离为10，且f（2）=0，若将函数f（x）的图象向右平移t（t＞0）的单位长度后所得函数图象关于y轴对称，则t的最小值为（ ）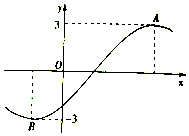
    A.1
    B.2
    C.3
    D.4

    【答案】C
    【解析】解：由题设图象知，周期 T=|AB|，解得：T=20， ∴ω= = ．
    可得f（x）=3sin（ +）
    ∵f（2）=0，
    ∴sin（ +）=0，
    ∵ Φ ，
    ∴= ．
    故得f（x）=3sin（ ﹣ ）
    将函数f（x）的图象向右平移t（t＞0）的单位可得：y=3sin[ ） ]=3in（ ），
    函数图象关于y轴对称，
    ∴ ，
    整理得：﹣t=7+10k，
    ∵t＞0，
    ∴当k=﹣1时，t的最小值为3．
    故选C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】关于函数f（x）=sin （2x﹣ ）（x∈R），给出下列三个结论： ①对于任意的x∈R，都有f（x）=cos （2x﹣ ）；
    ②对于任意的x∈in R，都有f（x+ ）=f（x﹣ ）；
    ③对于任意的x∈R，都有f（ ﹣x）=f（ +x）．
    其中，全部正确结论的序号是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数满足：集合中至少存在三个不同的数构成等比数列，则称函数是等比源函数．

    （）判断下列函数：①；②；③中，哪些是等比源函数？（不需证明）

    （）判断函数是否为等比源函数，并证明你的结论．

    （）证明： ， ，函数都是等比源函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=lnx+ ，m∈R，若对任意b＞a＞0， ＜1恒成立，则m的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如表：

    API

    [0，50]

    （50，100]

    （100，150]

    （150，200]

    （200，250]

    （250，300]

    ＞300

    空气质量

    优

    良

    轻微污染

    轻度污染

    中度污染

    中度重污染

    重度污染

    天数

    4

    13

    18

    30

    9

    11

    15


    （1）若某企业每天由空气污染造成的经济损失S（单位：元）与空气质量指数API（记为ω）的关系式为： S= 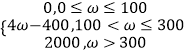，试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
    （2）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？ 附：

    P（K2≥k0）

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    k2=

    非重度污染

    重度污染

    合计

    供暖季

    非供暖季

    合计

    100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我市某矿山企业生产某产品的年固定成本为万元，每生产千件该产品需另投入万元，设该企业年内共生产此种产品千件，并且全部销售完，每千件的销售收入为万元，且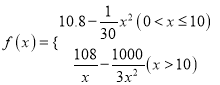

    （Ⅰ）写出年利润（万元）关于产品年产量（千件）的函数关系式；

    （Ⅱ）问：年产量为多少千件时，该企业生产此产品所获年利润最大？

    注：年利润=年销售收入-年总成本.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下，请根据此解答如下问题：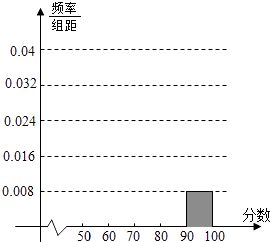

    （1）求班级的总人数；
    （2）将频率分布表及频率分布直方图的空余位置补充完整；
    （3）若要从分数在[80，100）之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90，100）之间的概率．

    分组

    频数

    频率

    [50，60）

    0.08

    [60，70）

    7

    [70，80）

    10

    [80，90）

    [90，100）

    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，函数.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若不等式在上恒成立，求实数a的取值范围；

    （Ⅲ）若，求证不等式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

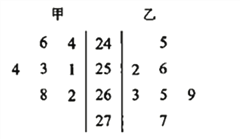
    【题目】双十一网购狂欢，快递业务量猛增．甲、乙两位快递员月日到日每天送件数量的茎叶图如图所示．

    （Ⅰ）根据茎叶图判断哪个快递员的平均送件数量较多（写出结论即可）；

    （Ⅱ）求甲送件数量的平均数；

    （Ⅲ）从乙送件数量中随机抽取个，求至少有一个送件数量超过甲的平均送件数量的概率．

    查看答案和解析>>

    同步练习册答案