

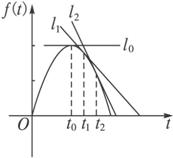
解:用曲线f(t)在t0,t1,t2处的切线刻画曲线f(t)在t0,t1,t2附近的变化情况.
(1)当t=t0时,曲线f(t)在t0处的切线l0平行于x轴.所以在t=t0附近曲线比较平坦,几乎没有升降.
(2)当t=t1时,曲线f(t)在t1处的切线l1的斜率f′(t1)<0,所以在t=t1附近曲线下降,即函数f(t)在t=t1附近单调递减.
(3)当t=t2时,曲线f(t)在t2处的切线l2的斜率f′(t2)<0,所以在t=t2附近曲线下降,即函数f(t)在t=t2附近也单调递减.由图象可以看出,直线l1的倾斜程度小于直线l2的倾斜程度,说明曲线f(t)在t1附近比在t2附近下降得缓慢.
(4)当t=2时,f(2)=0.
在t=2时的切线的斜率k=f′(2)=![]()
![]() ?
?
=![]()
![]()
=![]()
![]()
=![]() (-2Δt-4)=-4.
(-2Δt-4)=-4.
所以切线的方程为y=-4(x-2),
即4x+y-8=0.
点评:f(t)对t的导数即为在该点处的切线的斜率,应明确导数的几何意义.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:044

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com