
分析 (1)求出函数的导数,通过讨论b的范围,求出函数的单调区间即可;
(2)b=0时,求出h(x)的导数,得到2xlnx-x+a=0有两个不为a且不为1的相异实根,令φ(x)=2xlnx-x+a,结合函数的单调性求出a的范围即可.
解答 解:(1)∵f(x)的定义域为(0,+∞),
$f'(x)=\frac{1}{x}+b$,…(1分)
所以,当b≥0时,f'(x)>0,
∴f(x)在(0,+∞)单调递增.…(3分)
当b<0时,令f'(x)=0,
∴$x=-\frac{1}{b}$,$x∈({0\;\;,\;\;-\frac{1}{b}})$时,f'(x)>0,
∴f(x)在$({0\;\;,\;\;-\frac{1}{b}})$单调递增.
$x∈({-\frac{1}{b}\;\;,\;\;+∞})$时,f'(x)<0,
∴f(x)在$({-\frac{1}{b}\;\;,\;\;+∞})$单调递减.…(5分)
(2)当b=0时,$h(x)=\frac{{{{({x-a})}^2}}}{lnx}$.
$h'(x)=\frac{{2({x-a})lnx-\frac{{{{({x-a})}^2}}}{x}}}{{{{(lnx)}^2}}}=\frac{{({x-a})({2xlnx-x+a})}}{{x{{(lnx)}^2}}}$.…(6分)
∵h(x)有三个极值点,∴h'(x)=0有三个相异的实根.
所以2xlnx-x+a=0有两个不为a且不为1的相异实根.…(7分)
令φ(x)=2xlnx-x+a,φ'(x)=1+2lnx,令φ'(x)=0,
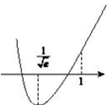
∴$x=\frac{1}{{\sqrt{e}}}$,列表得:
| x | $({0,\frac{1}{{\sqrt{e}}}})$ | $\frac{1}{{\sqrt{e}}}$ | $({\frac{1}{{\sqrt{e}}},1})$ | (1,∞) |
| φ'(x) | - | 0 | + | + |
| φ(x) | 单调递减 | 单调递增 | 单调递增 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,数形结合思想,是一道中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
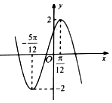
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①② | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
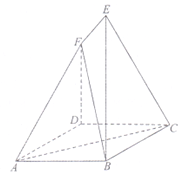 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3.084 | B. | 3.138 | C. | 3.142 | D. | 3.136 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{e}{2}$) | B. | ($\frac{e}{2}$,e) | C. | (0,e) | D. | (e,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com