练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：

    ①“若a、b∈R，则a－b＝0?a＝b”类比推出“若a、b∈C，则a－b＝0?a＝b”；

    ②“若a、b、c、d∈R，则复数a＋bi＝c＋di?a＝c，b＝d”类比推出；“若a、b、c、d∈Q，

    则a＋b＝c＋d?a＝c，b＝d”；

    ③“若a、b∈R，则a－b>0?a>b”类比推出“若a、b∈C，则a－b>0?a>b”；

    ④“若x∈R，则|x|<1?－1<x<1”类比推出“若z∈C，则|z|<1?－1<z<1”．

    其中类比结论正确的命题序号为________(把你认为正确的命题序号都填上)．

     

    【答案】

    ①②

    【解析】

    试题分析：根据题意，由于类比推理的概念可知，

    对于①“若a、b∈R，则a－b＝0?a＝b”类比推出“若a、b∈C，则a－b＝0?a＝b”；成立。

    对于②“若a、b、c、d∈R，则复数a＋bi＝c＋di?a＝c，b＝d”类比推出；“若a、b、c、d∈Q，

    则a＋b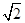＝c＋d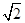?a＝c，b＝d”；成立。

    对于③“若a、b∈R，则a－b>0?a>b”类比推出“若a、b∈C，则a－b>0?a>b”；当a=2+3i，b=1+3i不成立，故错误。

    对于④“若x∈R，则|x|<1?－1<x<1”类比推出“若z∈C，则|z|<1?－1<z<1”．比如z=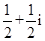不成立故答案为①②

    考点：命题真假的判定

    点评：主要是考查了命题的真假的判定，属于基础题。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下面类比推理命题（其中Q为有理数集，R为实数集，C为复数集）
    ①“若a，b∈R，则a-b=0?a=b”类比推出“若a，b∈C，则a-b=0?a=b”；
    ②“若a，b，c，d∈R，则复数a+bi=c+di?a=c，b=d”，类比推出“若a，b，c，d∈Q，则a+b
    		2
    =c+d
    		2
    ?a=c，b=d    ”；
    ③“若a，b∈R，则a-b＞0?a＞b”类比推出“若a，b∈C，则a-b＞0?a＞b”；
    ④“若x∈R，则|x|＜1?-1＜x＜1”类比推出“若x∈C，则|z|＜1?-1＜z＜1
    其中类比结论正确的个数是（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下面类比推理命题（其中Q为有理数集，R为实数集，C为复数集）：
    ①“若a，b∈R，则a-b=0⇒a=b”类比推出“若a，b∈C，则a-b=0⇒a=b”；
    ②“若a，b，c，d∈R，则复数a+bi=c+di⇒a=c，b=d”类比推出“若a，b，c，d∈Q，则复数b=d”
    ③“若a，b∈R，则a-b＞0⇒a＞b”类比推出“若a，b∈C，则a-b＞0⇒a＞b”
    其中类比得到的结论正确的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下面类比推理命题：
    ①“若a•3=b•3，则a=b”类推出“若a•0=b•0，则a=b”；
    ②“若（a+b）c=ac+bc”类推出“
    a+b
    c
    =
    a
    c
    +
    b
    c
    (c≠0)    ”；
    ③“（ab）n=anbn”类推出“（a+b）n=an+bn”；
    ④“ax+y=ax•ay（0＜a≠1）”类推出“loga（x+y）=logax•logay（0＜a≠1）”．
    其中类比结论正确的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下面类比推理命题（其中Q为有理数集，R为实数集，C为复数集），其中类比结论正确的是（　　）
    A、“若a，b∈R，则a2+b2=0⇒a=0且b=0”类比推出“若z1，z2∈C，则z12+z22=0⇒z1=0且z2=0”
    B、“若a，b，c，d∈R，则复数a+bi=c+di⇒a=c，b=d”类比推出“若a，b，c，d∈Q，则a+b
    		2
    =c+d
    		2
    ⇒a=c，b=d    ”
    C、“若a，b∈R，则a-b＞0⇒a＞b”类比推出“若z1，z2∈C，则z1-z2＞0⇒z1＞z2”
    D、“若x∈R，则|x|＜1⇒-1＜x＜1”类比推出“若z∈C，则|z|＜1⇒-1＜z＜1”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下面类比推理命题（其中Q为有理数集，R为实数集，C为复数集）：
    ①“若a、b∈R，则a-b=0⇒a=b”类比推出“a、，b∈C，则a-b=0⇒a=b”
    ②“若x∈R，则|x|＜1⇒-1＜x＜1”类比推出“若z∈C，则|z|＜1⇒-1＜z＜1”
    ③“若a、b、∈R，则a-b＞0⇒a＞b”类比推出“若a、b∈C，则a-b＞0⇒a＞b”
    其中类比结论正确的个数有（　　）

    查看答案和解析>>

    同步练习册答案