练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数，关于方程有三个不同实数解，则实数的取值范围为（    ）

    A．B．
    C．D．

    D

    解析试题分析：函数，根据的图象，设，∵关于x的方程有有三个不同的实数解，即为有两个根，且一个在上，一个在上．设，①当有一个根为时，，，此时另一根为，符合题意．②当没有根为时，则：，解得，综上可得，m的取值范围是．

    考点：对数函数图象与性质的综合应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    在对数函数中，下列描述正确的是（   ）
    ①定义域是、值域是R ②图像必过点(1,0).
    ③当时，在上是减函数；当时，在上是增函数.
    ④对数函数既不是奇函数，也不是偶函数.

    A．①②B．②③C．①②④D．①②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    函数的定义域是

    A．[1，2]B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若，则的大小关系为（    ） 

    A．<< B．<< C．<< D．<<

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若，则（）

    A． B． C． D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设，，，则(     )

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    函数f(x)=x2+lnx4的零点所在的区间是（   ）

    A．(0,1) B．(1,2) C．(2,3) D．(3,4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    定义在上的奇函数满足：当时，，则方程的实数根的个数是（   ）

    A．1 B．2 C．3 D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某工厂产生的废气经过过滤后排放，排放时污染物的含量不得超过1%．己知在过滤过程中废气中的污染物数量尸（单位：毫克／升）与过滤时间t（单位：小时）之间的函数关系为：P=P0e－kt，（k，P0均为正的常数）．若在前5个小时的过滤过程中污染物被排除了90%．那么，至少还需（ ）时间过滤才可以排放．

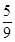    A．小时 B．小时 C．5小时 D．10小时

    查看答案和解析>>

    同步练习册答案